cs234-2: 马尔科夫奖励过程、Policy improvement
cs234-2: 马尔科夫奖励过程、Policy improvement
Sheldon ZhengLecture 2
MRP 马尔科夫奖励过程
\[ \begin{equation} \left(\begin{array}{c} V\left(s_1\right) \\ \vdots \\ V\left(s_N\right) \end{array}\right)=\left(\begin{array}{c} R\left(s_1\right) \\ \vdots \\ R\left(s_N\right) \end{array}\right)+\gamma\left(\begin{array}{ccc} P\left(s_1 \mid s_1\right) & \cdots & P\left(s_N \mid s_1\right) \\ P\left(s_1 \mid s_2\right) & \cdots & P\left(s_N \mid s_2\right) \\ \vdots & \ddots & \vdots \\ P\left(s_1 \mid s_N\right) & \cdots & P\left(s_N \mid s_N\right) \end{array}\right)\left(\begin{array}{c} V\left(s_1\right) \\ \vdots \\ V\left(s_N\right) \end{array}\right) \end{equation} \]
写成整式形式
\[ \begin{equation} \begin{aligned} V &=R+\gamma P V \\ V-\gamma P V &=R \\ (I-\gamma P) V &=R \\ V &=(I-\gamma P)^{-1} R \end{aligned} \end{equation} \]
只要γ<1则总是可逆的
如何计算MRP
- Dynamic programming
- Initialize \(V_0(s)=0\) for all \(s\)
- For \(k=1\) until convergence
- For all \(s\) in \(S\)
\[ V_k(s)=R(s)+\gamma \sum_{s^{\prime} \in S} P\left(s^{\prime} \mid s\right) V_{k-1}\left(s^{\prime}\right) \]
- Computational complexity: \(O\left(|S|^2\right)\) for each iteration \((|S|=N)\)
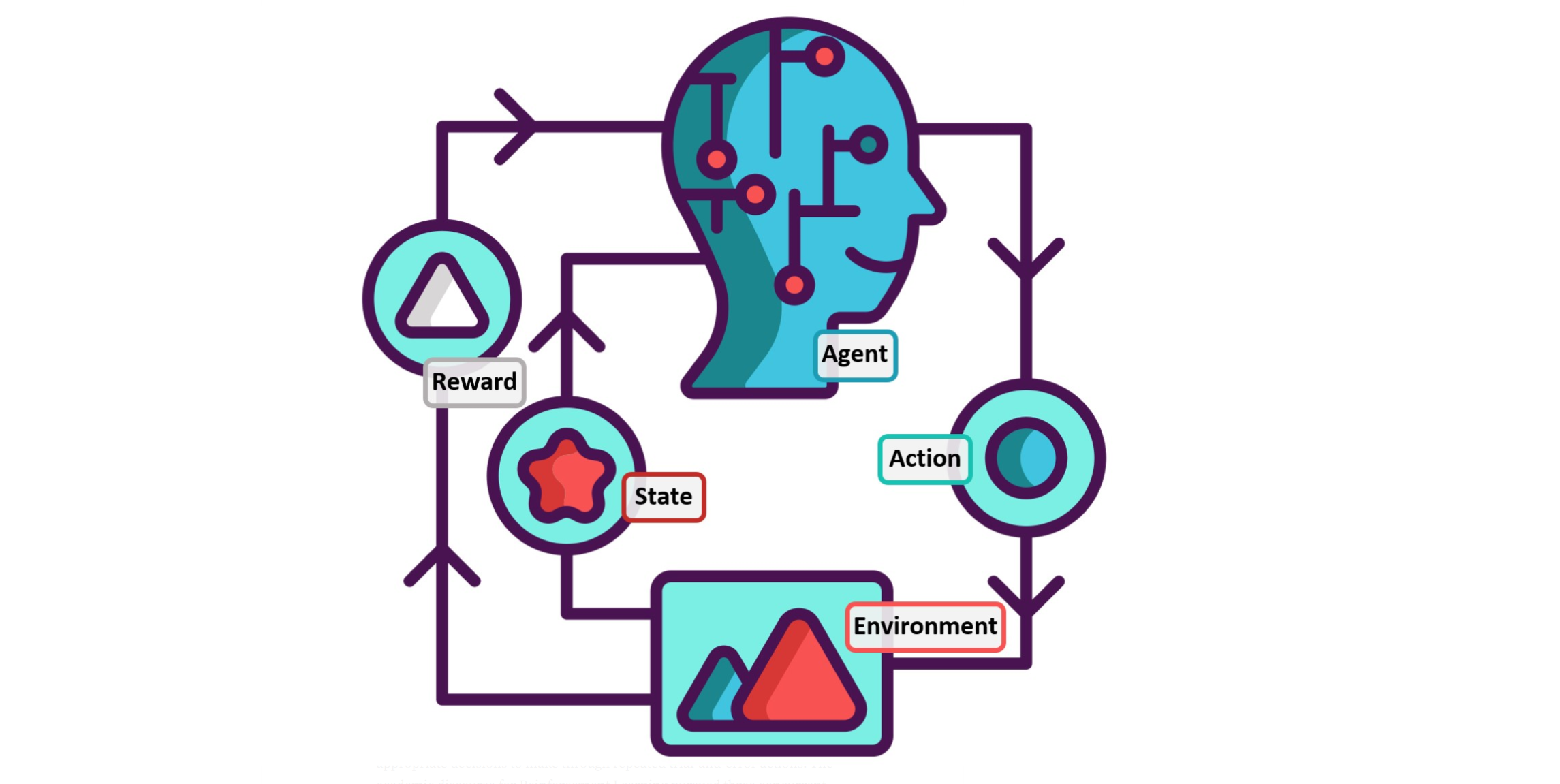
马尔科夫决策问题MDP 定义:
- Markov Decision Process is Markov Reward Process \(+\) actions
- Definition of MDP
- \(S\) is a (finite) set of Markov states \(s \in S\)
- \(A\) is a (finite) set of actions \(a \in A\)
- \(P\) is dynamics/transition model for each action, that specifies \(P\left(s_{t+1}=s^{\prime} \mid s_t=s, a_t=a\right)\)
- \(R\) is a reward function \({ }^1\)
\[ R\left(s_t=s, a_t=a\right)=\mathbb{E}\left[r_t \mid s_t=s, a_t=a\right] \]
- Discount factor \(\gamma \in[0,1]\)
- MDP is a tuple: \((S, A, P, R, \gamma)\)
马尔科夫决策和马尔科夫奖励过程
- \(\mathrm{MDP}+\pi(a \mid s)=\) Markov Reward Process
- Precisely, it is the MRP \(\left(S, R^\pi, P^\pi, \gamma\right)\), where
\[ \begin{aligned} R^\pi(s) &=\sum_{a \in A} \pi(a \mid s) R(s, a) \\ P^\pi\left(s^{\prime} \mid s\right) &=\sum_{a \in A} \pi(a \mid s) P\left(s^{\prime} \mid s, a\right) \end{aligned} \]
迭代法求状态
- Initialize \(V_0(s)=0\) for all \(s\)
- For \(k=1\) until convergence
- For all \(s\) in \(S\)
\[ V_k^\pi(s)=r(s, \pi(s))+\gamma \sum_{s^{\prime} \in S} p\left(s^{\prime} \mid s, \pi(s)\right) V_{k-1}^\pi\left(s^{\prime}\right) \]
- This is a Bellman backup for a particular policy
Deterministic policy & policy iteration
\(|A|^{|S|}\) 是policy的总数
- Set \(i=0\)
- Initialize \(\pi_0(s)\) randomly for all states \(s\)
- While \(i=0\) or \(\left\|\pi_i-\pi_{i-1}\right\|_1>0\)
(L1-norm, measures if the policy changed for any
state):
- \(V^{\pi_i} \leftarrow\) MDP \(V\) function policy evaluation of \(\pi_i\)
- \(\pi_{i+1} \leftarrow\) Policy improvement
- \(i=i+1\)
Policy improvement
Q值的定义:
\[ Q^{\pi_i}(s, a)=R(s, a)+\gamma \sum_{s^{\prime} \in S} P\left(s^{\prime} \mid s, a\right) V^{\pi_i}\left(s^{\prime}\right) \]
PI推导:通过得到最大Q值选出最优policy
\[ \begin{gathered} Q^{\pi_i}(s, a)=R(s, a)+\gamma \sum_{s^{\prime} \in S} P\left(s^{\prime} \mid s, a\right) V^{\pi_i}\left(s^{\prime}\right) \\ \max _a Q^{\pi_i}(s, a) \geq R\left(s, \pi_i(s)\right)+\gamma \sum_{s^{\prime} \in S} P\left(s^{\prime} \mid s, \pi_i(s)\right) V^{\pi_i}\left(s^{\prime}\right)=V^{\pi_i}(s) \\ \pi_{i+1}(s)=\arg \max _a Q^{\pi_i}(s, a) \end{gathered} \]
Monotonic improvement in policy 单调提升策略
定义:如果一个策略优于另一个策略,则该策略下所有状态值都要优于另一策略下所有状态值
\[ V^{\pi_1} \geq V^{\pi_2}: V^{\pi_1}(s) \geq V^{\pi_2}(s), \forall s \in S \]
- Proposition: \(V^{\pi_{i+1}} \geq V^{\pi_i}\) with strict inequality if \(\pi_i\) is suboptimal, where \(\pi_{i+1}\) is the new policy we get from policy improvement on \(\pi_i\)
策略\(\pi_{i}\) 是状态的期望值,小于等于最优动作的Q值:
\[ \begin{equation} \begin{aligned} V^{\pi_i}(s) & \leq \max _a Q^{\pi_i}(s, a) \\ &=\max _a R(s, a)+\gamma \sum_{s^{\prime} \in S} P\left(s^{\prime} \mid s, a\right) V^{\pi_i}\left(s^{\prime}\right) \end{aligned} \end{equation} \]
证明:
\[ \begin{aligned} V^{\pi_i}(s) & \leq \max _a Q^{\pi_i}(s, a) \\ &=\max _a R(s, a)+\gamma \sum_{s^{\prime} \in S} P\left(s^{\prime} \mid s, a\right) V^{\pi_i}\left(s^{\prime}\right) \\ &=R\left(s, \pi_{i+1}(s)\right)+\gamma \sum_{s^{\prime} \in S} P\left(s^{\prime} \mid s, \pi_{i+1}(s)\right) V^{\pi_i}\left(s^{\prime}\right) / / \text { by the definition of } \pi_{i+1} \\ & \leq R\left(s, \pi_{i+1}(s)\right)+\gamma \sum_{s^{\prime} \in S} P\left(s^{\prime} \mid s, \pi_{i+1}(s)\right)\left(\max _{a^{\prime}} Q^{\pi_i}\left(s^{\prime}, a^{\prime}\right)\right) \\ &=R\left(s, \pi_{i+1}(s)\right)+\gamma \sum_{s^{\prime} \in S} P\left(s^{\prime} \mid s, \pi_{i+1}(s)\right) \\ &\left(R\left(s^{\prime}, \pi_{i+1}\left(s^{\prime}\right)\right)+\gamma \sum_{s^{\prime \prime} \in S} P\left(s^{\prime \prime} \mid s^{\prime}, \pi_{i+1}\left(s^{\prime}\right)\right) V^{\pi_i}\left(s^{\prime \prime}\right)\right) \\ & \vdots \\ =& V^{\pi_{i+1}}(s) \end{aligned} \]
如果一个policy优化中不再改变,则该policy就再也不会改变
总结:通过优化Q值选出最优策略。
Value Iteration
\[ V^\pi(s)=R^\pi(s)+\gamma \sum_{s^{\prime} \in S} P^\pi\left(s^{\prime} \mid s\right) V^\pi\left(s^{\prime}\right) \]
Bellman backup operator
- Applied to a value function
- Returns a new value function
- Improves the value if possible
\[ B V(s)=\max _a R(s, a)+\gamma \sum_{s^{\prime} \in S} p\left(s^{\prime} \mid s, a\right) V\left(s^{\prime}\right) \]
值循环算法:
Set \(k=1\)
Initialize \(V_0(s)=0\) for all states \(s\) 初始化状态值
Loop until [finite horizon, convergence]: 有限循环直至收敛
- For each state \(s\)
\[ V_{k+1}(s)=\max _a R(s, a)+\gamma \sum_{s^{\prime} \in S} P\left(s^{\prime} \mid s, a\right) V_k\left(s^{\prime}\right) \]
- View as Bellman backup on value function
\[ \begin{gathered} V_{k+1}=B V_k \\ \pi_{k+1}(s)=\arg \max _a R(s, a)+\gamma \sum_{s^{\prime} \in S} P\left(s^{\prime} \mid s, a\right) V_k\left(s^{\prime}\right) \end{gathered} \]
提升每一个状态的状态值到收敛,然后得到最优policy
- 只要discount factor \(\gamma \lt 1\) ,或者结束在一个终端状态节点的概率为1就可以收敛
- bellman equation是contraction operator,前提是\(\gamma \lt 1\)
- 施加了Bellman equation的的两个不同的值函数,其距离会减小
Contraction operator
定义:
- Let \(O\) be an operator, and \(|x|\) denote (any) norm of \(x\)
- If \(\left|O V-O V^{\prime}\right| \leq\left|V-V^{\prime}\right|\), then \(O\) is a contraction operator
证明Bellman equation是一个压缩操作符
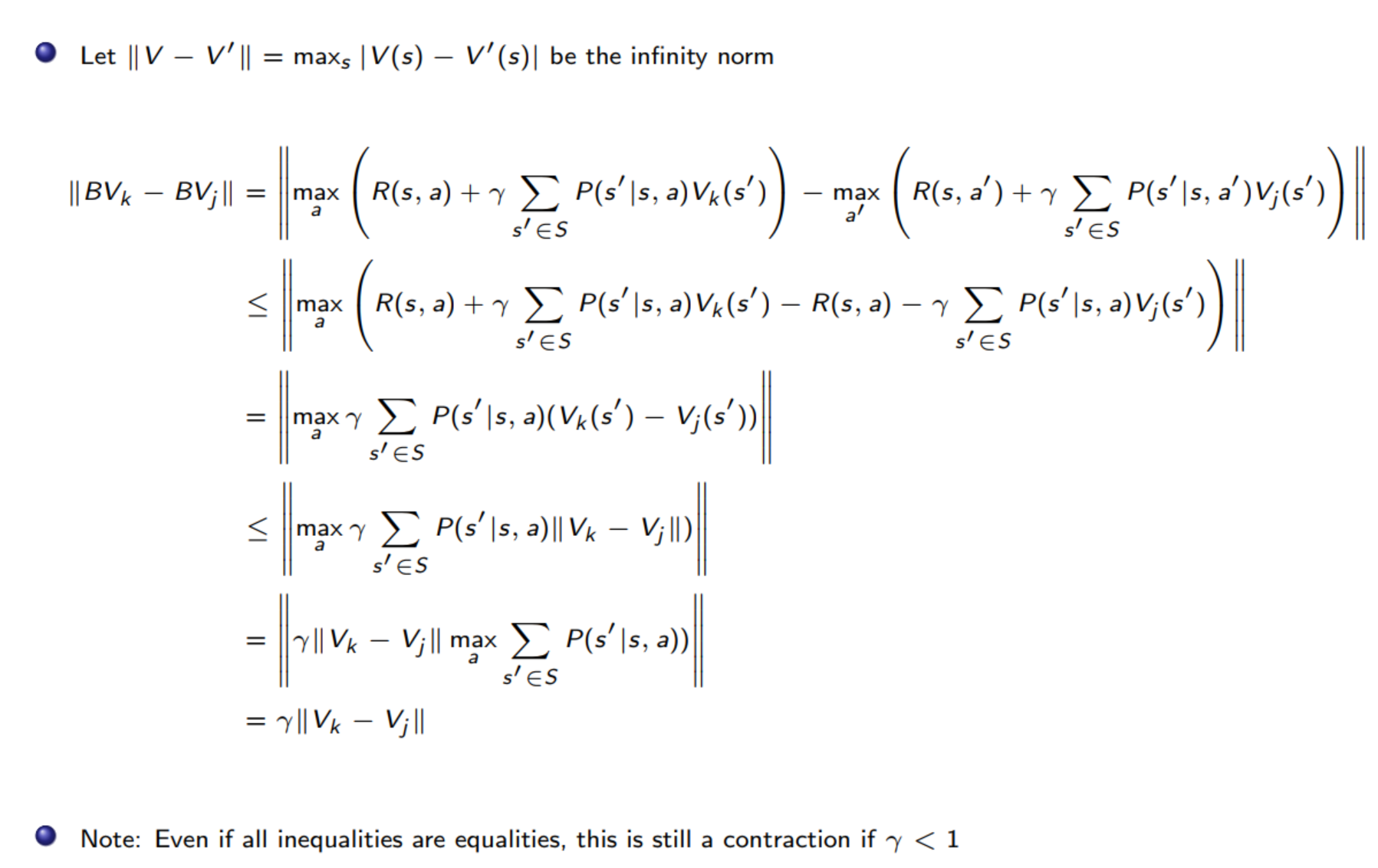
value iteration和 policy iteration的区别