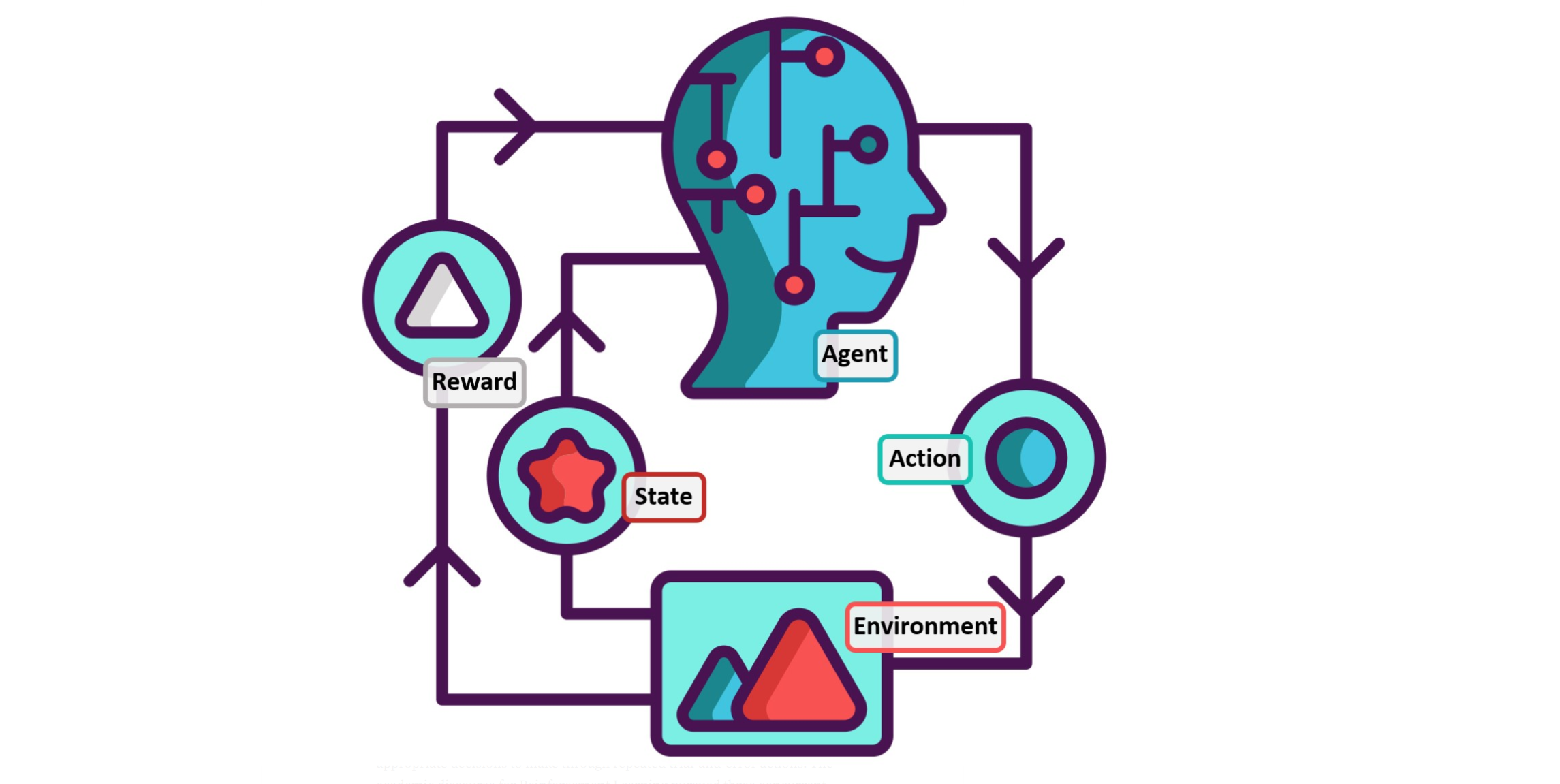
cs234-11: Fast Reinforcement Learning I
cs234-11: Fast Reinforcement Learning I
Sheldon ZhengMultiarmed Bandits问题
多臂老虎机问题
多臂老虎机是假设在玩一个拥有多个摇臂的老虎机,每个摇臂对应一个动作,玩家一次只能选取一个摇臂,相当于是选取了一个动作,描述如下:
- 老虎机有K个摇臂,每个摇臂以一定的概率吐出金币,且概率是未知的,但服从一定的概率分布即
- \[ \mathcal{R}^{a} (r) = \mathbb{P}[r|a] \]
- 玩家每次(每个时间步step)只能从K个摇臂中选择其中一个摇臂 \(a \in \mathcal{A}\),且相邻两次选择或奖励没有任何关系
- 环境会给出奖励
- \[ r_t \sim \mathcal{R}^{a_t} \]
- 玩家的目的是通过一定的策略使自己获得的累计奖励最大,即得到更多的金币
- \[ \sum_{\tau=1}^t r_\tau \]
贪心算法选取最优动作Greedy Algorithm
使用蒙特卡洛算法估计的动作值
\[ \hat{Q}_t(a)=\frac{1}{N_t(a)} \sum_{t=1}^T r_t \mathbb{1}\left(a_t=a\right)\\ \Rightarrow\\ \hat{Q}_t(a)=\frac{1}{N_t(a)} \sum_{t=1}^T r_t \mathbf{1}\left(a_t=a\right)=\hat{Q}_{t-1}(a)+\frac{1}{N_t(a)}\left(r_t-\hat{Q}_{t-1}(a)\right) \]
这里认为估计值约等于实际值
\[ \hat{Q}_t(a) \approx Q(a) \]
使用贪心算法可以得到最优动作,即从大的估计值中选取其对应的动作:
\[ a_t^*=\arg \max _{a \in \mathcal{A}} \hat{Q}_t(a) \]
但是这样有可能使得选取的最优动作并非全局最优,而是局限在局部最优,且由于视野范围有限,取决于实际的样本,可能永远无法跳出来局部的视野。
我们也可以采用\(\epsilon-greedy\)算法,让贪婪算法有一定概率(1-\(\epsilon\))去使用不是最优的动作,一定程度避免局部锁定,另外类似的还有\(decaying-\epsilon-greedy\) 算法,改变固定的\(\epsilon\).
Regret
regret从字面意思上指的是“遗憾”,在强化学习问题中指本可以得到的最大奖励和实际得到的奖励之间的差值。
几个概念:
Action-value: 对于使用某个动作\(a\)得到的平均奖励,多臂老虎机中指摇某个固定的臂所获得的平均奖励
\[ Q(a)=\mathbb{E}[r \mid a] \]
Optimal value \(V^{ *}\) : 在一步多臂老虎机游戏中能够获得的最优奖励,即摇动能够带来最多金币的臂所带来的奖励
\[ V^*=Q\left(a^*\right)=\max _{a \in \mathcal{A}} Q(a) \]
- Regret: 在一步游戏中丧失的机会
\[ I_t=\mathbb{E}\left[V^*-Q\left(a_t\right)\right] \]
- Total Regret : 在全局游戏中(摇过很多轮之后)累计丧失的机会: \[ L_t=\mathbb{E}\left[\sum_{\tau=1}^t V^*-Q\left(a_\tau\right)\right] \]
在多臂老虎机游戏中,最大化最大累计奖励就等于最小化累计Regret
衡量Regret
衡量Regret需要定义两个量:
- 一个是摇臂的次数Count = $ N_t(a)$
- 一个是实际摇臂动作\(a\)带来的奖励值和理论上的最优动作\(a^{*}\)所带来的最大奖励值之间的差值
- Gap \(\Delta_i = V^ {*}-Q(a_i)\)
Regret 就是由这两个量构成的函数
\[ \begin{aligned} L_t &=\mathbb{E}\left[\sum_{\tau=1}^t V^{*}-Q\left(a_\tau\right)\right] \\ &=\sum_{a \in \mathcal{A} } \mathbb{E}\left[N_t(a)\right]\left(V^*-Q(a)\right) \\ &=\sum_{a \in \mathcal{A} } \mathbb{E}\left[N_t(a)\right] \Delta_a \\ &=\sum_{a \in \mathcal{A} } \bar{N}_t(a) \Delta_a \end{aligned} \]
即累计的Regret是由每一步的最优动作值减去实际动作值的加和的期望,最后以Gap和Count的形式给出,上式最后一项计算total regret,可以看出total regret由每个动作的选取次数的平均值乘以该动作的gap值的累加形成。
A good algorithm ensures small counts for large gap, but gaps are not known
Regret bound
对于类似贪心算法一类的算法,需要进行对其优劣性的衡量,此时就需要用到regret bound
regret bound有两个类型:
- 是总步数T的函数,界定函数总步数的regret范围
- 是对每一个action的选择次数和选择的动作间reward gap的函数
Lower Bound下限
- 界定问题的难度
- 算法的性能由最优动作和其他动作的相似性决定
- 较难的问题拥有相似的动作集,但动作的均值不同
- 描述lower bound的正式形式是gap \(\Delta_a\)和KL-离散度分布,\(D_{KL}(\mathcal{R^{a}||R^{a^{*}}})\)
定理:
渐进的total regret 至少是关于时间步的对指数相关的:
Theorem 1 (Lai and Robbins, 1985). Any algorithm on a MAB has an asymptotic lower bound on total rearet of at least
\[ \lim _{t \rightarrow \infty} L_t \geq {\log t} \sum_{a \mid \Delta_a>0} \frac{\Delta_a}{D_{KL}\left(\mathcal{R}^a \| \mathcal{R}^{a^*}\right)} \]
Upper Confidence Bounds (UCB)置信上界
UCB 是指对于每个动作值,都有一个上限置信边界,这个边界在任何时刻都大于等于该动作值。
UCB取决于对于一个动作选取的次数,选取动作选取能够最大化UCB的动作:
\[ a_t=\arg \max _{a \in \mathcal{A}}\left[U_t(a)\right] \]
Hoeffding's Inequality 霍夫丁不等式
规定一个Upper confidence \(\hat{U}_t(a)\) , 这个不是界,只是一个常量
\[ a_t=\arg \max _{a \in \mathcal{A}}\left\{\hat{Q}_t(a)+\hat{U}_t(a)\right\} \]
Theorem (Hoeffding's Inequality): Let \(X_1, \ldots, X_n\) be i.i.d. random variables in \([0,1]\), and let \(\bar{X}_n=\frac{1}{n} \sum_{\tau=1}^n X_\tau\) be the sample mean. Then
\[ \mathbb{P}\left[\mathbb{E}[X]>\bar{X}_n+u\right] \leq \exp \left(-2 n u^2\right) \]
在上式中,${X}_n +u \(是sample mean+\)u$, \(u\)只是一个常量,代表的意思是真实的期望值大于样本期望值加一个常量的概率小于等于\(exp(-2nu^2)\) ,
将霍夫定不定式应用在动作值则有:
\[ \mathbb{P}\left[Q(a)>\hat{Q}_t(a)+\hat{U}_t(a)\right] \leq \exp \left(-2 N_t(a) \hat{U}_t(a)^2\right) \]
则意思是真实的动作\(a\)的Q值大于采样值\(\hat{Q_t}(a)\) 加上一个置信上界值\(U_t(a)\)的概率小于右边部分\(\exp \left(-2 N_t(a) u^2\right)\),由于右边也含有置信上界,则可以赋予其一个概率求得这个置信上界\(U_t(a)\).
如果此时令\(\exp \left(-2 N_t(a) u^2\right)\)等于\(p\)
\[ \begin{aligned} \exp \left(-2 N_t(a) \hat{U}_t(a)^2\right) &=p \\ \hat{U}_t(a) &=\sqrt{\frac{-\log p}{2 N_t(a)}} . \end{aligned} \]
一般取概率\(p = t^{-4}\) 则得出UCB1的算法选出最优动作:
\[ a_t=\arg \max _{a \in \mathcal{A}}\left\{Q(a)+\sqrt{\frac{2 \log t}{N_t(a)}}\right\} \]
如果令\(p=\exp \left(-2 N_t(a) \hat{U}_t(a)^2\right)={\delta t^{-2}}\),则有:
\[ \exp \left(-2 N_t(a) \hat{U}_t(a)^2\right)= \frac{\delta}{t^2}\\\\ \Longrightarrow \hat{U}_t(a) = \sqrt{\frac{1}{2 n} \log \left (\frac{t^2}{\delta}\right)} \]
那么我们可以反推得到,令样本的均值加上一个置信上界后大于等于真实动作值的概率至少为
\[ \mathbb{P}\left[\hat{Q}_t(a)+\hat{U}_t(a)\geq Q(a) \right] \geq 1-\frac{\delta}{t^2} \]
其中\(t\)是步数,\(\delta\)是一个常量表示小概率
这时就可以得到一个置信上界\({U}_t(a_t)\)
\[ U_t\left(a_t\right)=\hat{Q}\left(a_t\right)+\sqrt{1 / 2 N_t(a) \cdot \log \left(1^2 / \delta\right)} \]
UCB算法可以实现渐进的总regret
Theorem 3 (Auer et al., 2002, [2]). The UCB algorithm achieves asymptotic total regret
\[ \lim _{t \rightarrow \infty} L_t \leq 8 \log t \sum_{a \mid \Delta_a>0} \Delta_a \]
共轭分布
在贝叶斯统计中,如果后验分布与先验分布属于同类(分布形式相同),则先验分布与后验分布被称为共轭分布,而先验分布被称为似然函数的共轭先验。

- 似然函数 (Likelihood) : 关于统计模型中的参数 \(\theta\) 的函数,表示模型参数中的似然性
- 先验分布 (Prior):在未看到观测数据的时候参数 \(\theta\) 的不确定性的概率分布
- 后验分布 (Posterior):考虑和给出相关证据或数据后所得到的条件概率分布
- 分母 \(\left(\int p(D \mid \theta) p(\theta) d \theta\right)\) : 可以理解为是正则化,使得最终概率相加为 1 ,符合基本约束的 作用 在贝叶斯定理中,参数先有一个先验认知 (先验分布),然后通过观察新数据,得到后验认知(后验分布)。
二项分布和Beta分布是共轭分布(转自知乎)