Log-Barrier-method

在求一些优化问题的时候，往往遇到形式如下的问题：

\[ \begin{array}{lll} \text { Problem statement } & h: \mathbb{R}^{n_x} \rightarrow \mathbb{R}^{n_h} \\ \min _{x \in \mathbb{R}^{n_x}} & f(\boldsymbol{x}) & \boldsymbol{g}: \mathbb{R}^{n_x} \rightarrow \mathbb{R}^{n_g} \\ \text { subject to: } & \boldsymbol{h}(\boldsymbol{x})=\mathbf{0} & \\ & \boldsymbol{g}(\boldsymbol{x}) \leq \mathbf{0} \end{array} \]

即需要满足\(x\)在\(h(x)\) 上且 \(g(x) \leq 0\) 时最小化\(f(x)\) 的值。

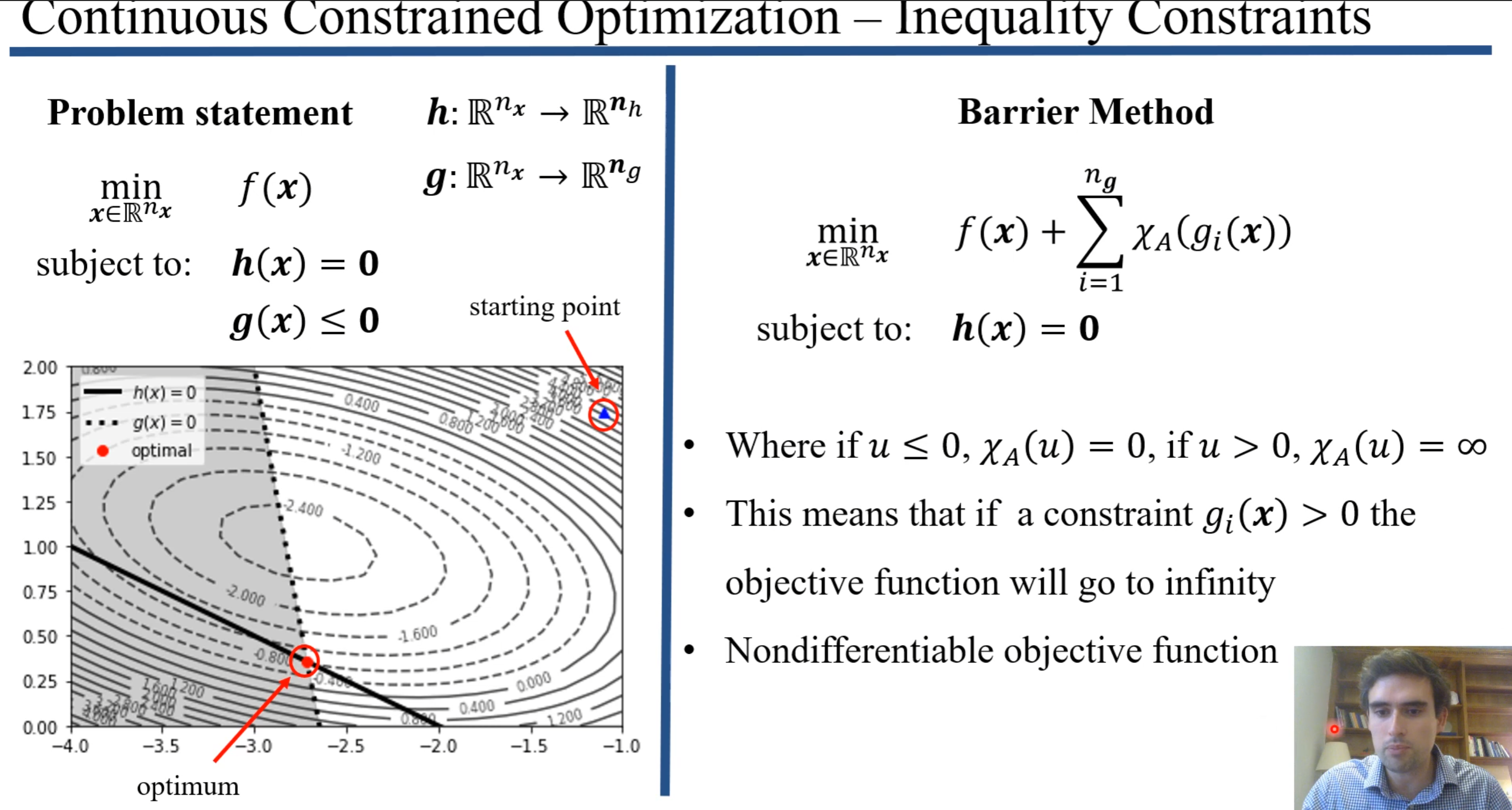
采用barrier的方法可以求得此解，具体做法是将constraint \(g(x) \leq 0\) 以累加的方式套入到一个选取的函数\(\mathcal{X}_{A}(u)\) 中，然后加到\(f(x)\)后面，最后计算最小化整个公式。 \(\mathcal{X}_{A}(u)\) 则满足性质如果\(u \leq 0\) 则\(\mathcal{X}_{A}(u) = 0\) ，此时最小化整个式子则等同于直接最小化\(f(x)\); 如果\(u \geq 0\) ，则整个式子将随着累加号指数\(i\)的增加会趋向于正无穷；

选取\(-\frac{1}{t}log(-u)\) 作为 \(\mathcal{X}_{A}(u)\) 满足上述条件，且当 \(g_i{(x)}^{-} \rightarrow 0\) 时 \(\log \left(-g_i(x)\right) \rightarrow-\infty\) ，且\(-\log \left(-g_i(\boldsymbol{x})\right) \rightarrow \infty\)

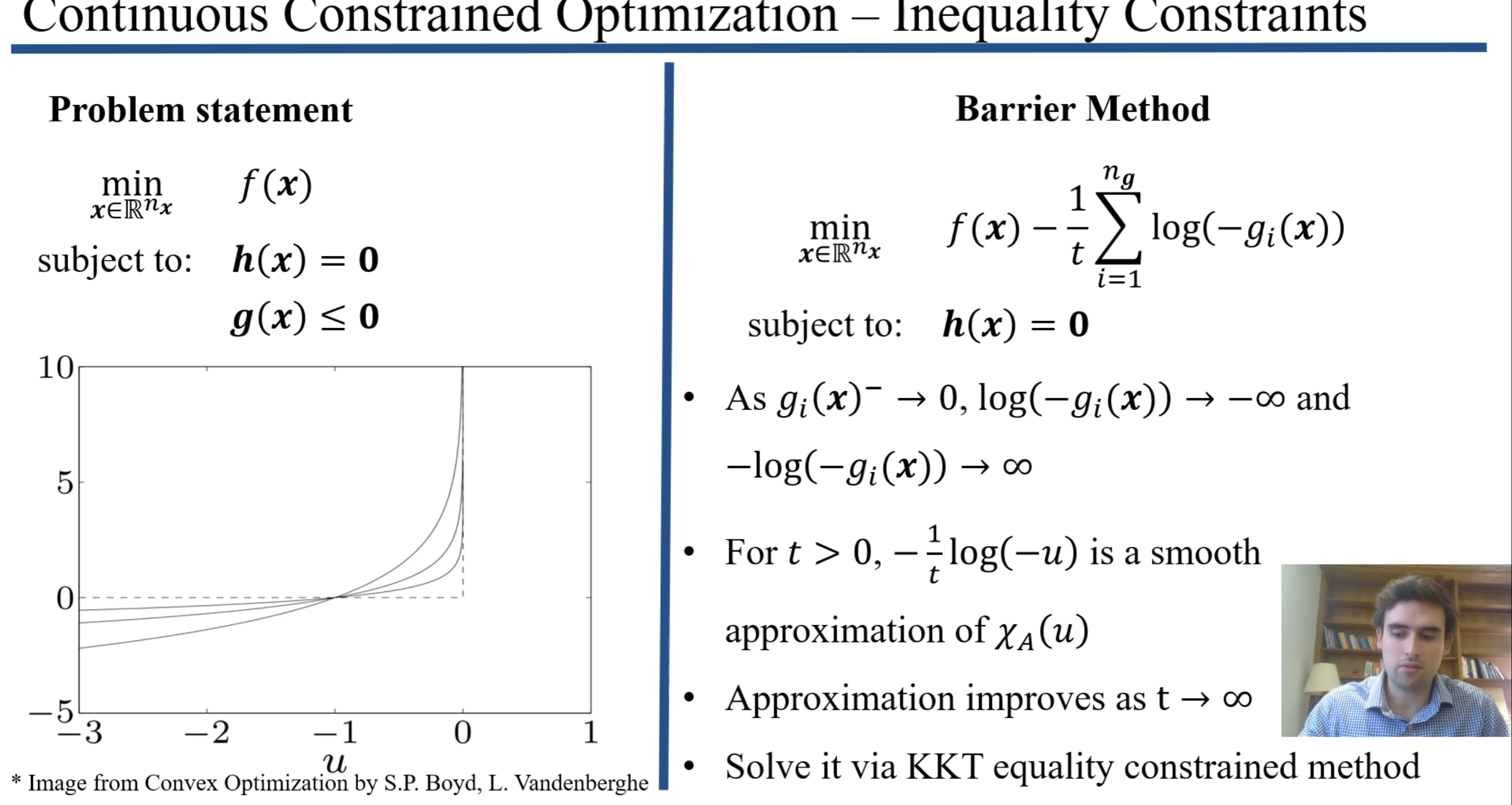
因此，对于\(t>0,\) \(-\frac{1}{t} \log (-u)\) 是对\(\mathcal{X}_{A}(u)\) 的光滑估计，并随着\(t \rightarrow \infty\) 估计值越靠近

Central path

如果单纯地取一个很大的\(t\) 值有时候并不能解决问题，因为过大的数值\(t\)会导致\(x\)在数值求解上的难度和不稳定性；正确的方法是先取一个小\(t\) 值，然后得到一个尽量大的\(x^{\star}\) ,然后增大\(t\),再从\(x^{\star}\)开始继续优化，这样不断交叉，走出来的\(x\)轨迹称之为central path