Key	Value
文献类型	journalArticle
标题	Many-Agent Reinforcement Learning
中文标题	多代理强化学习
作者	[Yaodong Yang]
评分	⭐⭐⭐⭐⭐
分类	[[A 多智能体增强学习, 0 综述]]
条目链接	My Library
PDF 附件	2021__Yang__Many-Agent Reinforcement Learning.pdf

👣➿👣

Alpha rank :

Mathmatical formulation

假设有\(N\)个agent，每个agent有\(k_i\)个策略，则有

• 单个智能体的策略集 \(\mathscr{S}_i\) , 大小为\(k_i\)： \(\mathscr{S}_i=\left\{\pi_{i, 1}, \ldots, \pi_{i, k_i}\right\}, k_i=\left|\mathscr{S}_i\right|\)
• 联合策略集(joint strategy set) \(\mathscr{S}_{joint}\): 所有智能体的所有策略构建成，大小为\(k^N\)：\(\mathscr{S}_{\text {joint }}=\mathscr{S}_1 \times \mathscr{S}_2 \times \cdots \times \mathscr{S}_N\)
• 联合策略配置（joint strategy profile） \(\pi_{joint}\) : 所有智能体的某个策略组成集合，大小为N： \(\pi_{\text {joint }}=\left\{\pi_{1, j_1}, \ldots, \pi_{N, j_N}\right\}\) with \(\pi_{i, j_i} \in \mathscr{S}_i\) and \(j_i \in\left\{1, \ldots, k_i\right\}\).

Mathematical Formulation: To formalise \(\alpha\)-Rank, we consier \(N\) agents each, denoted by \(i\), having access to a set of strategies of size \(k_i\). We refer to the strategy set for agent \(i\) by \(\mathscr{S}_i=\left\{\pi_{i, 1}, \ldots, \pi_{i, k_i}\right\}, k_i=\left|\mathscr{S}_i\right|\), with \(\pi_{i, j}: \mathscr{X} \times \mathscr{A}_i \rightarrow[0,1]\) representing the \(j^{\text {th }}\) allowed policy of the learner. \(\mathscr{X}\) represents the set of states, and \(\mathscr{A}_i\) is the set of actions for agent \(i\). A joint strategy profile is a set of policies for all participating agents in the joint strategy set, i.e., \(\mathscr{S}_{\text {joint }}=\mathscr{S}_1 \times \mathscr{S}_2 \times \cdots \times \mathscr{S}_N\) : \(\pi_{\text {joint }}=\left\{\pi_{1, j_1}, \ldots, \pi_{N, j_N}\right\}\), with \(\pi_{i, j_i} \in \mathscr{S}_i\) and \(j_i \in\left\{1, \ldots, k_i\right\}\). We assume \(k=k_1=\) \(\ldots=k_N\) hereafter.

联合策略配置回报函数： 所有联合策略的回报函数

\[ \mathscr{P}_{\text {joint }}=\left\{\mathscr{P}_1\left(\pi_{\text {joint }}\right), \ldots, \mathscr{P}_N\left(\pi_{\text {joint }}\right)\right\} \]

联合策略配置变换概率： agent \(i\) 的策略\(a\)变成策略集中另一个策略\(b\)的概率，agent \(i\)策略a变成不属于策略集中的策略\(c\)的概率

\[ \begin{aligned} &\mathbb{P}\left(\pi_{i, a} \rightarrow \pi_{i, b}, \boldsymbol{\pi}_{-i}\right)=\frac{e^{\alpha \mathscr{P}_i\left(\pi_{i, b}, \pi_{-i}\right)}}{e^{\alpha \mathscr{P}_i\left(\pi_{i, a}, \pi_{-i}\right)}+e^{\alpha \mathscr{P}_i\left(\pi_{i, b}, \pi_{-i}\right)}}-\frac{\mu}{2} \\ &\quad \text { for }\left(\pi_{i, a}, \pi_{i, b}\right) \in \mathscr{S}_i \times \mathscr{S}_i, \\ &\mathbb{P}\left(\pi_{i, a} \rightarrow \pi_{i, c}, \boldsymbol{\pi}_{-i}\right)=\frac{\mu}{k_i-2}, \quad \forall \pi_{i, c} \in \mathscr{S}_i \backslash\left\{\pi_{i, a}, \pi_{i, b}\right\}, \end{aligned} \]

联合策略转移矩阵： 对于联合策略集可以通过图进行联合策略配置转移矩阵的定义，即为：\(\mathcal{T} \in \mathbb{R}^{k^{N} \times k^{N}}\) ，这个二维矩阵如果用块表示的话可以表示为\(N\times N\)，横轴纵轴分别为agent编号，每一个块内表示对应的配置变换概率。

\[ T \in \mathbb{R}^{\left|\mathscr{S}_{\text {joint }}\right| \times\left|\mathscr{S}_{\text {joint }}\right|} \]

联合策略变换概率 ：种群中个体a入侵另一除去b的种群的概率

\[ \rho_{\pi_{i, a}, \hat{\pi}_{i, b}}\left(\boldsymbol{\pi}_{-i}\right)=\frac{1-e^{-\alpha\left(\mathscr{P}_i\left(\pi_{i, a}, \boldsymbol{\pi}_{-i}\right)-\mathscr{P}_i\left(\hat{\pi}_{i, b}, \boldsymbol{\pi}_{-i}\right)\right)}}{1-e^{-m \alpha\left(\mathscr{P}_i\left(\pi_{i, a}, \boldsymbol{\pi}_{-i}\right)-\mathscr{P}_i\left(\hat{\pi}_{i, b}, \boldsymbol{\pi}_{-i}\right)\right)}}, \]

定义两个不同的联合策略中不止一个策略是不同的概率为0

Now we restrict our attention to variations in joint policies involving more than two individual strategies, i.e., \(\left|\boldsymbol{\pi}_{\text {joint }} \backslash \hat{\boldsymbol{\pi}}_{\text {joint }} \geq 2\right|\). Here we set \([\boldsymbol{T}]_{\boldsymbol{\pi}_{\text {joint }}, \hat{\boldsymbol{\pi}}_{\text {joint }}}=0\)

则有：

\[ [\boldsymbol{T}]_{\boldsymbol{\pi}_{\text {joint }}, \hat{\boldsymbol{\pi}}_{\text {joint }}}=\left\{\begin{array}{l} \frac{1}{\sum_{l=1}^N\left(k_l-1\right)} \rho_{\pi_{i, a}, \hat{\pi}_{i, b}}\left(\boldsymbol{\pi}_{-i}\right), \text { if }\left|\boldsymbol{\pi}_{\text {joint }} \backslash \hat{\boldsymbol{\pi}}_{\text {joint }}\right|=1, \\ 1-\sum_{\hat{\boldsymbol{\pi}} \neq \boldsymbol{\pi}_{\text {joint }}}[\boldsymbol{T}]_{\boldsymbol{\pi}_{\text {joint }}, \hat{\boldsymbol{\pi}}}, \text { if } \boldsymbol{\pi}_{\text {joint }}=\hat{\boldsymbol{\pi}}_{\text {joint }}, \\ 0, \quad \text { if }\left|\boldsymbol{\pi}_{\text {joint }} \backslash \hat{\boldsymbol{\pi}}_{\text {joint }}\right| \geq 2 \end{array}\right. \]

Ranking matrix：

以及一个稳定分布\(\mathcal{v} \in \mathbb{R}^{k^{N}}\) 这个分布表示的是联合策略的级别，用于评估联合策略配置中的策略，即每一个策略的可能性也就是其被选择的概率。

Alpha-rank意义

那么这个概率的满足\(\bf{\mathcal{Tv}} = \mathcal{v}\) ,就是概率分布稳定不会变了，解决这个公式求得概率分布就得到了策略的ranking.

The goal in \(\alpha\)-Rank is to establish an ordering in policy profiles dependent: on evolutionary stability of each joint strategy. In other words, higher ranked strategies are these that are prevalent in populations with higher average time of survival.”

alpha-rank的意义是在不同的联合策略集的不演变中，对其中的联合策略进行打分，得分高的策略就证明该策略在种群演化的过程中存在时间很长，也就是其进化的稳定性较好。

alpha rank的目的就是求解这个特征向量\(v\)，最后该向量中的每一个元素都代表了其对应的联合策略在进化过程中的稳定性。

可以通过对\(\boldsymbol{v}=\lim _{t \rightarrow \infty}\left[[\boldsymbol{T}]^T\right] \boldsymbol{v}_0\) 进行求解得到，此处\(v_0\)是一个初始分布，\(v\)是一个稳态分布，可以将该问题转化为求特征向量问题

\[ [\boldsymbol{T}]^T \boldsymbol{v}=\boldsymbol{v} \]

算法如下

但是由于alpha rank的时间复杂度太高，在现实中不具备求解方法；作者使用几种方法来估算其时间复杂度，并使用了算力和金钱的比喻来揭示其复杂度过高。

Power method 估计复杂度 通过使用power method的方法可以更新得出来\(T\)矩阵，但是这种方法的重要缺陷是其本身就是指数型的复杂度，最后得出使用power method的方法的复杂度为：

\[ \mathscr{O}(m)=\mathscr{O}(n[k N-N+1]) \approx \mathscr{O}\left(k^N k N\right) \]

此外还有其他方法的复杂度：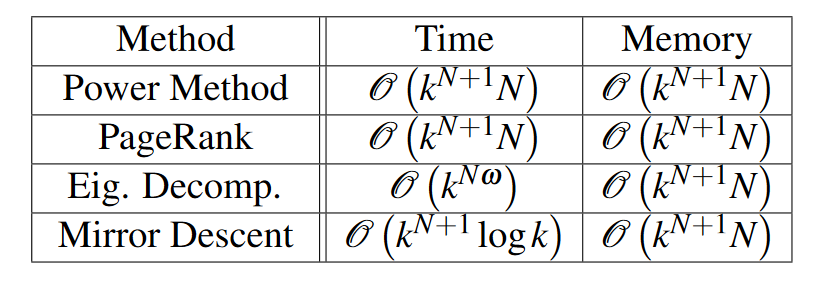

对于\(\alpha\) rank,作者用金钱花费来计量得到所有联合策略的回报矩阵的花销，印证用当前方法找到\(v\)是不现实的：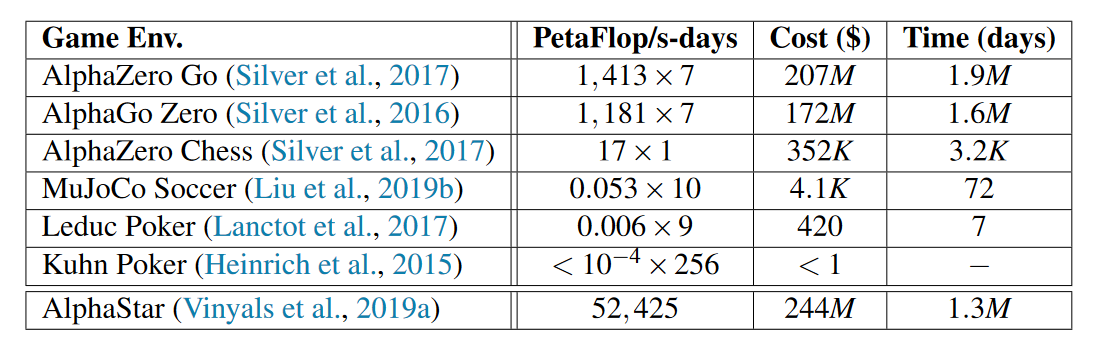

\(\alpha^{\alpha}\) rank

如何找到\(v\)呢？首先根据\(T^{T}x=x\) ,对于矩阵\(x\)的求解可以转化为优化问题：

\[ \begin{equation} \min _{\boldsymbol{x}} \frac{1}{n}\left\|||\boldsymbol{T}^T \boldsymbol{x}-\boldsymbol{x}\right\|||_2^2 \text { s.t. } \boldsymbol{x}^T \mathbf{1}=1, \text { and } \boldsymbol{x} \succeq \mathbf{0} \end{equation} \]

又有：

\[ \frac{1}{n}\left\|||\boldsymbol{T}^T \boldsymbol{x}-\boldsymbol{x}\right\|||_2^2=\frac{1}{n} \sum_{i=1}^n\left(\boldsymbol{x}^T \boldsymbol{b}_i\right)^2 \]

然后引入log barrier method便可以对其进行进一步转化，变为求最小值优化问题：

\[ \min _{x \in \mathbb{R}^n} \frac{1}{n} \sum_{i=1}^n\left(\boldsymbol{x}^T \boldsymbol{b}_i\right)^2-\lambda \log \left(\delta^2-\left[x^T \mathbf{1}-1\right]^2\right)-\frac{\lambda}{n} \sum_{i=1}^n \log \left(x_i\right) . \]

Log-Barrier-method

求解上述log-barrier minimisation问题，作者使用了随机梯度的方法，即对log-barrier公式进行求导得到每一个i对应的梯度

\[ \nabla_{\boldsymbol{x}} f_{i_t}\left(\boldsymbol{x}_t\right)=2\left(\boldsymbol{b}_{i_t}^{\boldsymbol{T}} \mathbf{1}\right) \boldsymbol{b}_{i_t}+\frac{2 \lambda_t\left(\boldsymbol{x}_t^T \mathbf{1}-1\right)}{\boldsymbol{\delta}^2-\left(\boldsymbol{x}_t^T \mathbf{1}-1\right)^2}-\frac{\boldsymbol{\lambda}_t}{n}\left[\frac{1}{\left[\boldsymbol{x}_t\right]_1}, \ldots, \frac{1}{\left[\boldsymbol{x}_t\right]_n}\right]^T \]

其中\(\lambda_{t+1}=\frac{\lambda_t}{\gamma}\) 是一个定义的惩罚因子，随部署增加而变小；

通过执行梯度下降就可以不断对\(x\)取值进行优化，即

\[ \boldsymbol{x}_{t+1}=\boldsymbol{x}_t-\eta_t \nabla_{\boldsymbol{x}} f_{i_t}\left(\boldsymbol{x}_t\right) \]

最后就可以得到 \(\boldsymbol{v}\) 的近似解\(\boldsymbol{\hat{v}}\)

\(\alpha^{\alpha}\) oracle

除此以外，作者还使用了oracle方法分阶段地优化当前最优解，具体方法就是首先只从每个agent的策略集中选取一部分策略当做当前策略集\(\mathscr{S}_{i}^{[k]}, k\in {0,1,2...}\)

然后先 计算所有agent的策略集\(\mathscr{S}_{i}^{[k]}\) 可以产生的总的联合策略配置数量\(n=\prod_{i=1}^N\left|\mathscr{S}_i^{[k]}\right|\) 使用\(\alpha\) rank 的方法找到在T次迭代后当前最优的联合策略 \(\pi_{joint}^{top}\)

由于之前分割了每个agent的策略，只取用了每个agent的一部分策略组成总的策略集空间，所以当前的最优联合策略\(\pi_{joint}^{top}\) 只能说是在探索\(T\)步和由\(\mathscr{S}_{i}^{[k]}\) 组成的部分策略空间的前提下的最优，因此需要oracle算法进行进一步的遴选，以防止最后结果落入全局策略空间的局部最优。具体做法是：

当\(\alpha^{\alpha}\)rank在进行完一组迭代后，使用rank级别最高的当前最优策略\(\pi_{joint}^{[p],top}\) ,针对每一个agent \(i\) ，通过公式：

\[ \pi_i^{\star}=\arg \max _{\pi_i \in \mathscr{S}_i} \mathbb{E}_{\pi_i, \pi_{-i}^{\mathrm{top}}}\left[\sum_{h \geq 0} \gamma_i^h \mathscr{P}_i\left(\boldsymbol{s}_h, \boldsymbol{u}_{i, h}, \boldsymbol{u}_{-i, h}\right)\right], \]

寻找agent \(i\) 在其完整策略集\(\mathscr{S}_{i}\) 中相对于其他agent在当前最优策略\(\pi_{joint}^{[p],top}\) 下的最优策略，简而言之就是其他agent使用策略\(\pi_{joint}^{[p],top}\) 时寻找agent \(i\) 在策略集\(\mathscr{S}_{i}\) 中的最优策略\(\pi_i^{\star}\)，并将\(\pi_i^{\star}\)加入到分割策略集\(\mathscr{S}_{i}^{[k]}\) 中去进行对\(\mathscr{S}_{i}^{[k]}\) 的更新 。 值得注意的是，如果没有对\(\mathscr{S}_{i}\)进行初始化的采样，即\(\left\{\mathscr{S}_i^{[0]}\right\} \triangleq\left\{\mathscr{S}_i\right\}\) 时，\(\alpha^{\alpha}\)-Oracle就退化成为\(\alpha\) rank算法。