Single-Agent RL

Markov process 马尔科夫过程

马尔科夫过程是一个标准模型，广泛应用在全观测状态系统中，即智能体可以完全获取环境的状态信息，通过概率转换模型，在某一个状态通过一个动作到达另一个状态。因此结局马尔科夫问题的关键就是找到一个策略使得动作空间\(A\)映射到状态空间\(S\)上去。其中动作为\(a_{t} \sim \pi\left(\cdot \mid s_{t}\right)\) ，并能使得到达每一个状态获取的回报discounted accumulated reward能够被最大化：

\[ \mathbb{E}\left[\sum_{t \geq 0} \gamma^{t} R\left(s_{t}, a_{t}, s_{t+1}\right) \mid a_{t} \sim \pi\left(\cdot \mid s_{t}\right), s_{0}\right] \]

其中action-value function（Q方程）和state-value function (V方程)分别为：

\[ \begin{aligned} Q_{\pi}(s, a) &=\mathbb{E}\left[\sum_{t \geq 0} \gamma^{t} R\left(s_{t}, a_{t}, s_{t+1}\right) \mid a_{t} \sim \pi\left(\cdot \mid s_{t}\right), a_{0}=a, s_{0}=s\right] \\ V_{\pi}(s) &=\mathbb{E}\left[\sum_{t \geq 0} \gamma^{t} R\left(s_{t}, a_{t}, s_{t+1}\right) \mid a_{t} \sim \pi\left(\cdot \mid s_{t}\right), s_{0}=s\right] \end{aligned} \]

增强学习的智能体不需要知道模型的知识，RL agent是通过自身和环境互动的经验（observation/experience）去学习一个最优策略，大的方面增强学习可以分为两种：value-based和policy-based。

Value-based method

• Q learning:

\[ \hat{Q}(s, a) \leftarrow(1-\alpha) \hat{Q}(s, a)+\alpha\left[r+\gamma \max _{a^{\prime}} \hat{Q}\left(s^{\prime}, a^{\prime}\right)\right] \]

• Monte-Carlo tree search (MCTS): 通过构建蒙特卡洛搜索树来进行最优值函数的估计：

  • UCB1: upper confidence bound
  • UCT
  • non-asymptotic convergence

• Temporal difference

  • policy evaluation

Policy-based method

Policy-based method是直接搜索策略空间，通常是由参数化方程估算器，比如神经网络估算\(\pi(\cdot \mid s) \approx \pi_{\theta}(\cdot \mid s)\) （初始化一个函数，然后不断优化\(\theta\)参数来逼近真实的策略函数），最直接的方法就是沿着长期回报的梯度方向进行优化更新参数，被称之为policy gradient method（PG）：

\[ \begin{equation} \nabla J(\theta)=\mathbb{E}_ {a \sim \pi_{\theta}(\cdot \mid s), s \sim \eta_{\pi_{\theta}}(\cdot)}\left[Q_{\pi_{\theta}}(s, a) \nabla \log \pi_{\theta}(a \mid s)\right] \end{equation} \]

where \(J(\theta)\) and \(Q_{\pi_{\theta}}\) are the expected return and Q-function under policy \(\pi_{\theta}\), respectively, \(\nabla \log \pi_{\theta}(a \mid s)\) is the score function of the policy, and \(\eta_{\pi_{\theta}}\) is the state occupancy measure, either discounted or ergodic, under policy \(\pi_{\theta}\).

常见的方法有：

• REINFORCE
• G(PO)MDP
• actor-critic algorithms

Multi-agent RL framework

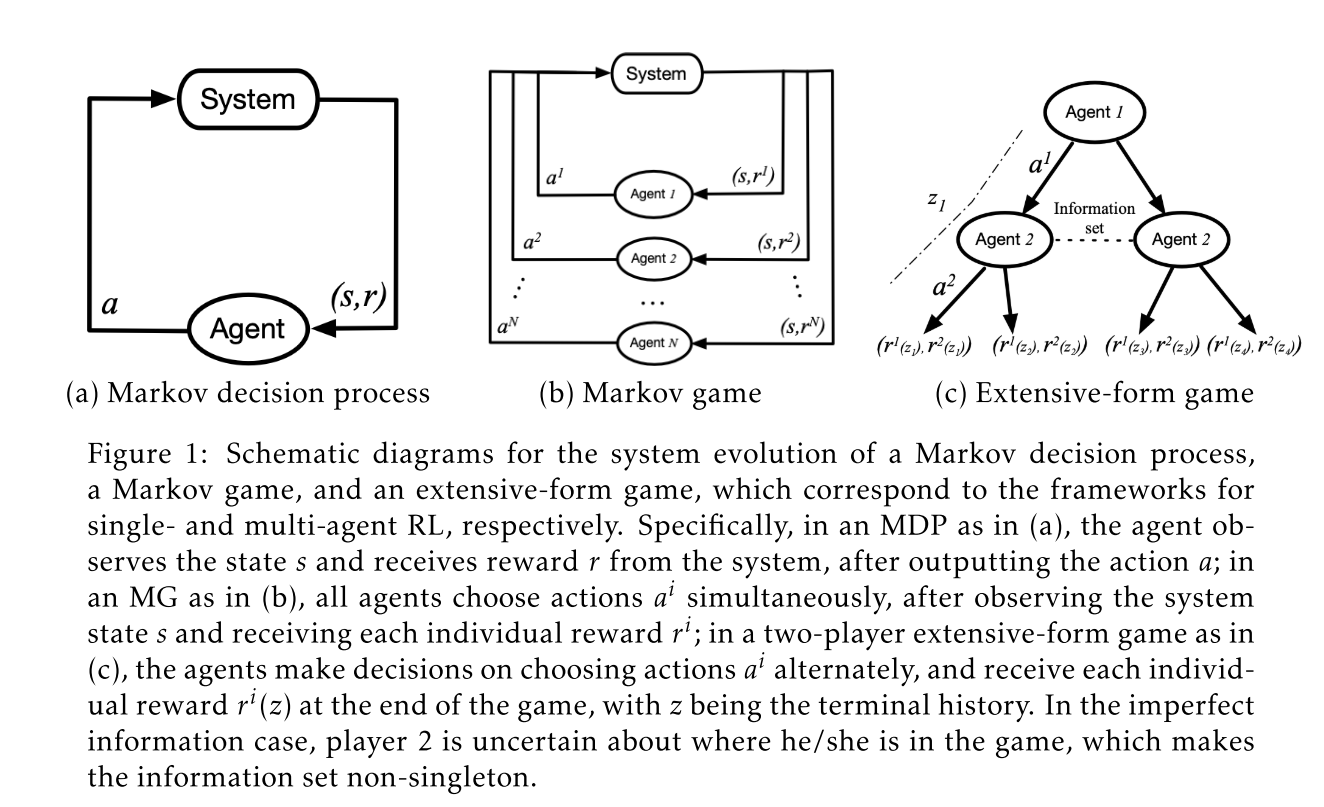
Markov Stotchatic Games （MG/MSG）马尔科夫游戏

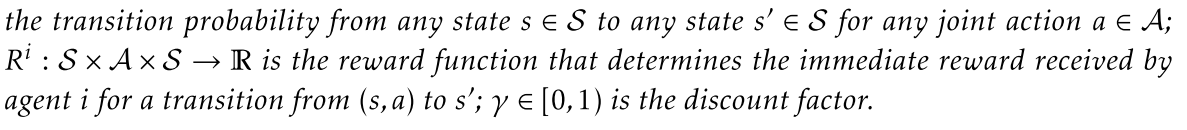
在时间\(t\)，每一个智能体agent \(i \in \mathcal{N}\) 执行一个动作\(a_t^{i}\)，对应系统的状态\(s_t\)。然后系统从状态\(s_t\)转变到状态\(s_{t+1}\)，并且对于每一个智能体agent \(i\) 都有奖励为\(R^{i}\left(s_{t}, a_{t}, s_{t+1}\right)\).

每一个智能体\(i\) 的目标是通过找到策略 \(\pi^{i}: \mathcal{S} \rightarrow \Delta\left(\mathcal{A}^{i}\right)\)使得动作\(a_{t}^{i} \sim \pi^{i}\left(\cdot \mid s_{t}\right)\)优化其自己的长期奖励(long-term reward)，作为结果，原本智能体 agent \(i\) 的状态-数值函数\(V^{i}: \mathcal{S} \rightarrow \mathbb{R}\) 的对应关系则变成了状态策略对应关系 \(\pi: \mathcal{S} \rightarrow \Delta(\mathcal{A})\) 定义为\(\pi(a \mid s):=\prod_{i \in \mathcal{N}} \pi^{i}\left(a^{i} \mid s\right)\)，特别的对于任意联合策略\(\pi\)和状态\(s\in \mathcal{S}\) 有：

\[ \begin{equation} V_{\pi^{i}, \pi^{-i}}^{i}(s):=\mathbb{E}\left[\sum_{t \geq 0} \gamma^{t} R^{i}\left(s_{t}, a_{t}, s_{t+1}\right) \mid a_{t}^{i} \sim \pi^{i}\left(\cdot \mid s_{t}\right), s_{0}=s\right] \end{equation} \]

上式中，\(\pi^{-i}\)代表除了\(i\)以外其他智能体的策略。

马尔科夫游戏区别于马尔科夫过程，因为一个智能体的最优选择不仅被其自身的策略所影响，同样被其他智能体的选择所影响。最常见的解决思想就是纳什均衡：

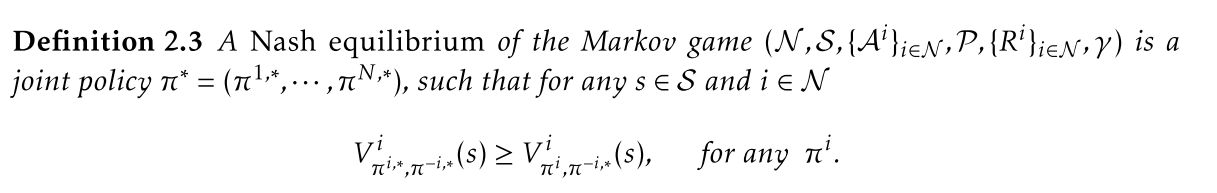
纳什均衡的基本意义就是所有的智能体都没理由或者额外的利益离开均衡点\(\pi^*\) ，纳什均衡总是存在于有限空间、无限时间的不连续马尔科夫游戏(MG)中，但是总的来说不是唯一的，有可能出现不同的均衡点。

在马尔科夫游戏模型中，可以有不同的基础设定种类。

• Cooperative Setting 协同设定基础：

  • Common reward ：

    • Multi-agent MDPs(MMDP):
    • 所有的智能体使用相同的回报函数：\(R^{1}=R^{2}=\cdots=R^{N}=R\)
    • 在此模型下，Q-function和value-function是完全相同的

  • Team-average reward：

    • 每一个agent可以保有自己的私有回报函数

    • 统一的合作目标是优化长期回报，这个回报的定义为：

      \(\bar{R}\left(s, a, s^{\prime}\right):=N^{-1} \cdot \sum_{i \in \mathcal{N}} R^{i}\left(s, a, s^{\prime}\right)\) for any \(\left(s, a, s^{\prime}\right) \in \mathcal{S} \times \mathcal{A} \times \mathcal{S}\).

    • 均值回报允许模型存在更多的异质性，同时可以允许每个agent能够保留一定程度的隐私，是一种去中心化的MARL算法

    • 但均值回报模型必须要有足够的沟通协议和沟通效率分析来支撑其异质性

• Competitive Setting 竞争设定：

  • 竞争设定总的来说是模拟马尔科夫游戏中的一种零和游戏（zero-sum）。即一方对奖励回报的获得代表另一方对其的失去，使用公式表达为：\(\sum_{i \in \mathcal{N}} R^{i}\left(s, a, s^{\prime}\right)=0\) for any \(\left(s, a, s^{\prime}\right)\)
  • 用于鲁棒学习，因为不确定性对系统的干扰或破坏可以模拟为游戏中的一个恶意的对手，纳什均衡获得的鲁棒策略可以优化最差长期回报。

• Mixed Setting 混合设定 ：

  • general-sum:没有明确的目标和关系束缚智能体，每一个智能体都是自我关心的，且其回报有可能是和其他智能体有所冲突的。
  • 比如两队智能体，既是对外零和也是对内合作。

Extensive Form Games 其他类型框架

马尔科夫游戏有一个比较大的限制就是其只能应用在fully observed的状态空间中，即每一个智能体都能够获得完美的全局信息，包括系统状态\(s_t\), 执行的动作\(a_t\)，以及时间\(t\)。

对于partial observability，即智能体只能获取一部分不完美的信息这样的游戏框架模型，称之为extensive-form games.

这部分不是主流

Challenges in MARL

Non-unique learning goals 没有明确的学习目标

• 学习目标可能是多维度的
• 纳什均衡是一个合理地多智能体的理想学习目标。对于纳什均衡来说，其目的是在算法收敛的时候找到一个均衡点，令所有的agent都不会偏离该点（即所有的agent的最佳利益点是这个均衡点），但是这需要两个前提：
  • 所有的agent都是理性的，也就是说不会干违背自己利益的事情
  • 所有的agent都有能力完美地进行推理和无限地彼此建模（即计算资源不受限）
• 现实中，agent往往只具备bounded rationality，即不一定能够完美地只做有益于自己的事情（比如人类，可能自己干的事从长远来看未必是利己的，比如破坏环境，发明原子弹，劈腿等等），况且现实中很难达到agent拥有无限或充足的计算资源去完成自己想要做的事情。
• 往往总体实现的目标并非是设计算法去找到一个完美的纳什均衡点，而是分为以下两种：
  • 针对特定的agent设计一个最佳的学习策略
  • 在game中（此处game并非游戏的意思，而是指代类似于游戏的一种过程）设计一类固定的其他类型的agents
• 收敛并不一定是绝对的目标，在value-based MARL算法中未必能够收敛到稳定的纳什均衡点，所谓的循环平衡的概念就是agent严格循环地通过一组稳定点地策略，也就是不收敛到任何纳什均衡点地策略。因此可以将学习目标分为stable和rational两种：
  • stable：确保算法可以收敛，前提是定义一组对立的对手agents
  • rational：在其他agent保持在stationary状态的时候可以保证agent收敛到一种 best-response的状态
  • 如果同时stable和rational，自然就可以收敛到纳什均衡的状态。
• 可以用一个regret的指标来表示agents的rationality，即计量算法与拥有后见之明的静态策略的性能的差异

Non-stationarity 没有稳态

因为多智能体增强学习在很多时候是同时进行的，智能体之间在独立学习的同时还在互相影响着其他智能体的回报函数的学习过程，在本质上这其实是违背了对于单个智能体在强化学习时的马尔可夫假设，即每一个智能体的状态都只有前一个状态决定。因此，基于马尔可夫假设的多智能体强化学习算法都有可能就没有一个稳定的收敛态，

A Survey of Learning in Multi-agent Environments: Dealing with Non-Stationarity

Cooperative Setting

Coopeartive setting 意思就是智能体之间互相合作，分享学习到的经验，最后整个智能体群通过算法迭代能够达到整体收敛的状态。

合作模式包含了异质和同质智能体之分，同质就是说所有智能体都一样，完成相同的任务，采取相同的回报函数，和一致性协同较类似；异质性指的是智能体之间各自使用不同的回报函数，每个智能体之间存在差异，可能完成的小目标也不尽相同，但是总体的大目标是一样的，称之为联合最优策略（optimal joint policy）

Decentralized Paradigm

QD-learning algorithm

QD算法是第一个可收敛的MARL算法，称为QD-learning，QD-learning 包含了共识（consensus）和创新（innovation）两部分，更新公式如下：

\[ \begin{gathered} Q_{t+1}^{i}(s, a) \leftarrow Q_{t}^ {i}(s, a)+\alpha_{t, s, a}\left[R^{i} (s, a)+\gamma \max_{a^ {\prime} \in \mathcal{A}} Q_{t}^{i}\left(s^{\prime}, a^{\prime}\right)-Q_{t}^{i}(s, a)\right] \\ -\beta_{t, s, a} \sum_{j \in \mathcal{N}_ {t}^{i}}\left[Q_{t}^{i}(s, a)-Q_{t}^{j}(s, a)\right] \end{gathered} \]

除了传统的TD-Q 部分，QD学习还增加了每个节点和周围邻居节点的Q估值的差值更新（\(\beta\)部分），用两个参数\(\alpha\)和\(\beta\)进行调节，可以保证收敛为最优Q函数。

Actor-critic algorithm

actor-critic 算法是一种去中心化算法，分为两步，第一步称之为actor step，第二步是critic步。

actor步骤由每个agent单独执行，不需要推断其他agent的策略。 另一方面，对于critic步骤，每个agent将其对价值函数value function的估计与网络上的邻居共享，从而实现共识估计，并在后续的actor步骤中进一步使用 。

the actor step is performed individually by each agent without the need to infer the policies of others. For the critic step, on the other hand, each agent shares its estimate of the value function with its neighbors on the network, so that a consensual estimate is achieved, which is further used in the subsequent actor step.

每个agent先将其自身的策略给参数化为：

\[ \pi_{\theta^{i}}^{i}: \mathcal{S} \rightarrow \Delta\left(\mathcal{A}^{i}\right) \text { by some parameter } \theta^{i} \in \mathbb{R}^{m^{i}} \text {, } \]

策略梯度为：

\[ \nabla_{\theta^{i}} J(\theta)=\mathbb{E}\left[\nabla_{\theta^{i}} \log \pi_{\theta^{i}}^{i}\left(s, a^{i}\right) \cdot Q_{\theta}(s, a)\right] \]

其中\(Q_{\theta}\)是在策略\(\pi_{\theta}\)下全局价值函数，\(\pi_{\theta}(a \mid s):=\prod_{i \in \mathcal{N}} \pi_{\theta^{i}}^{i}\left(a^{i} \mid s\right)\)，而\(\nabla_{\theta^{i}} \log \pi_{\theta^{i}}^{i}\left(s, a^{i}\right)\) 是局部得分函数（local score function）表征每一个agent的策略收益，尽管Q函数无法表征每一个agent单独的价值，但是通过将其参数化，使用一个参数\(w^i\),将\(Q_{\theta}(s,a)\) 变成\(Q_{\theta}(s,a,w^{i})\) ，然后在critic步骤运用consensus-based TD learning对其更新：

\[ \widetilde{\omega}_ {t}^{i}=\omega_{t}^{i}+\beta_{\omega, t} \cdot \delta_{t}^{i} \cdot \nabla_{\omega} Q_{t}\left(\omega_{t}^{i}\right), \quad \omega_{t+1}^{i}=\sum_{j \in \mathcal{N}} c_{t}(i, j) \cdot \widetilde{\omega}_ {t}^{j} \]

Finite-sample analyses 有限样本分析

不管是QD还是AC，都是在无限时间/步数的假设下最终收敛的。对于有限时间/步数的讨论主要有batch RL algorithm，即依旧是使用batch samples的形式对去中心化的Q函数变体进行拟合，著名方法有FQI。

Decentralized variant of Fitted-Q iteration (FQI)

• 在函数估计上使用深度神经网络

• 合作模式下，通过拟合目标价值函数的非线性最小平方来对所有的agents迭代地更新全局Q函数估计量

• 通过解决下式，使得所有的agent共同寻找一个普通Q-function估计

  • \(f \in \mathcal{F}\)是一系列Q函数的估计函数

  • 大小为n的状态转换样本，对所有agent可用:

    \[ \begin{equation} \{(s_{j},\{a_{j}^ {l}\}_ {i \in \mathcal{N}}, s_{j}^{\prime})\}_{j \in[n]} \end{equation} \]

  • local reward samples private to agent : \(\\{r_{j}^{i}\\}_ {j \in[n]}\)

  • local target value: \(y_{j}^ {i}=r_{j}^{i}+\gamma \cdot \max_{a \in \mathcal{A}} Q_{t}^{i}\left(s_{j}^{\prime}, a\right)\)

  • 最后对Q函数的估计可以通过解决下式得到：

  • \[ \min_{f \in \mathcal{F}} \frac{1} {N} \sum_{i \in \mathcal{N}} \frac{1} {2 n} \sum_{j=1}^{n}\left[y_{j}^{i}-f\left(s_{j}, a_{j}^{1}, \cdots, a_{j}^{N}\right)\right]^{2} \]

  FQI 存在的问题：

  • 如果初始的一系列估计函数\(\mathcal{F}\)使得每个agent的目标值和估计值之差的平方和是凸函数，即\(\sum_{j=1}^{n}\left[y_{j}^{i}-f\left(s_{j}, a_{j}^{1}, \cdots, a_{j}^{N}\right)\right]^{2}\)是凸的，则全局最优可以实现，但是在有限的迭代次数限制下，依旧会产生偏差，这个偏差导致Q函数的估计无法达到最优状态。
  • 对于最后Q函数估计的精度，主要取决于三个因素，即估计函数\(\mathcal{F}\), 迭代次数\(t\)和每次迭代的样本数量\(n\)。

Policy Evaluation

policy evaluation task，就是actor-critic 步骤中的critic步骤。

重要的几个方法：

1. MSPBE 方法

   • 所有agent的目标是联合最小化和团队平均回报相关的mean square projected Bellman error MSPBE

   • \(\min_{\omega} \quad \operatorname{MSPBE}(\omega):=\left\|\Pi_{\Phi}\left(V_{\omega}-\gamma P^{\pi} V_{\omega}-\bar{R}^{\pi}\right)\right\|_ {D}^{2}=\|A \omega-b\|_{C^{-1}}^{2}\)

     • 其中 \(\Pi_{\Phi}: \mathbb{R}^{|\mathcal{S}|} \rightarrow \mathbb{R}^{|\mathcal{S}|}\) 定义为 \(\Pi_{\Phi}:=\Phi\left(\Phi^{\top} D \Phi\right)^{-1} \Phi^{\top} D\) 是在子空间\(\\{\Phi \omega: \omega \in \mathbb{R}^{d}\\}\)的投影算子
     • $ A:= \{(s)^{}\}$
     • \(C:=\mathbb{E}\left[\phi(s) \phi^{\top}(s)\right]\)
     • \(b:=\) \(\mathbb{E}\left[\bar{R}^{\pi}(s) \phi(s)\right]\).

   • 可以转化为saddle point problem：\(\min_{\omega} \max_{\lambda^{i}, i \in \mathcal{N}} \frac{1} {N n} \sum_{i \in \mathcal{N}} \sum_{j=1}^{n} 2\left(\lambda^{i}\right)^{\top} A_{j} \omega-2\left(b_{j}^{i}\right)^{\top} \lambda^{i}-\left(\lambda^{i}\right)^{\top} C_{j} \lambda^{i}\)

   • 154，156，157，95，96，204

   • 156：分布式 gradient TD-based method + ODE

   • 96 double averaging scheme + dynamic consensus 205 + SAG algorithm 206

   • variance reduction 204

   • AVRG + TD-based 207

   • finite sample analyses 95, 157

   • distributed TD(0) 95

   • finite time + TD(\(\lambda\)) 157

2. independent agents and independent MDP

   • off-policy evaluation 154
   • TD-learning+ time varying communication network--- GTD2+TDC 211
   • indenpendent MDP setting 204

3. 其他的学习目标

   • optimal consensus problem 213
   • consensus error objective -- cooperative multi-agent graphical games 214
   • communication efficiency 130,131,132
   • distributed actor-critic 131