Passive reinforcement learning 被动增强学习

前提：

1. 环境有限，完全可观测，就是说所有的规则都掌握，在环境里所有动作所带来的作用都能够被识别。
2. 对于agent而言，有一个固定的动作执行策略\(\pi(s)\)，即在某种环境状态下执行某种动作
3. agent 的目标是学习贴现效用函数\(U^\pi(s)\)(discounted utility function) ，这里的\(s\)指的是状态，\(\pi\)是agent的执行策略

贴现效用函数\(U^\pi(s)\)(discounted utility function) ：从初始状态s开始执行策略\(\pi\) 的奖励之和的期望值

4x3 世界模型

使用一个4X3世界的Typical trials 做解释

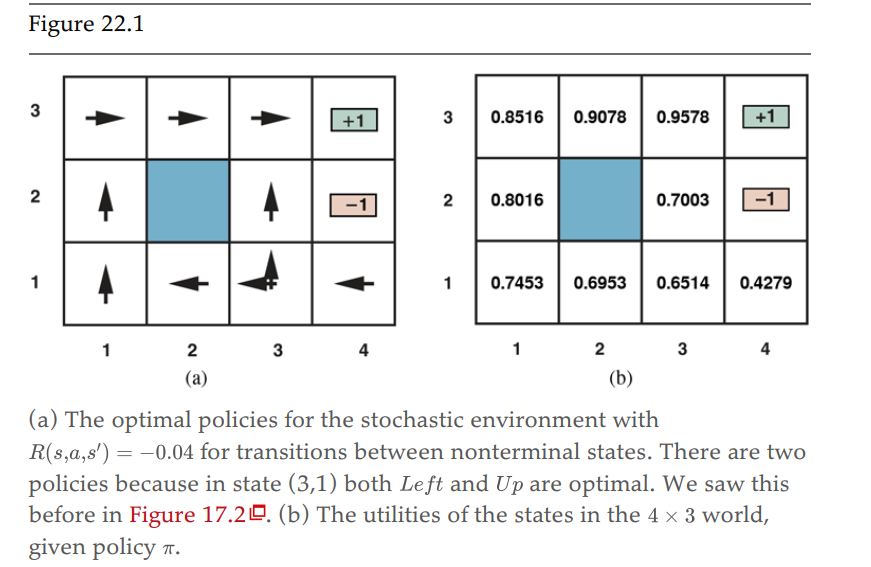
最上面3行是3个trails，即从(1,1)走到terminal states的三组走法，概率转换模型为图b所示，这是一个MDP问题，即有概率转换模型、reward、以及状态效用值。

简而言之，被动增强学习是指在某个可被观测的环境中，agent由初始状态\(s\)按照策略\(\pi\)学习效用函数\(U^\pi(s)\)的过程。

\[ U^{\pi}(s)=E\left[\sum_{t=0}^{\infty} \gamma^{t} R\left(S_{t}, \pi\left(S_{t}\right), S_{t+1}\right)\right] \]

公式中$\gamma^{t}$是在每一时刻$t$时的discount factor，$R\left(S_{t}, \pi\left(S_{t}\right), S_{t+1}\right)$是在状态$S_t$时进行动作$\pi(S_{t})$并得到状态$S_{t+1}$的奖励。

Direct Utility estimation

\[ U_{i}(s)=\sum_{s^{\prime}} P\left(s^{\prime} \mid s, \pi_{i}(s)\right)\left[R\left(s, \pi_{i}(s), s^{\prime}\right)+\gamma U_{i}\left(s^{\prime}\right)\right] \]

直接效用值估算是通过运行很多次trail，实现对状态效用值的直接估算。这样就相当于把增强学习变成了标准的有监督学习，但是显而易见，这样的缺点是需要运行很多次trials，本质上还是通过统计的方式把状态空间遍历，通过reward反馈和概率转换模型计算得出状态的效用值。而且，这种方法有一个很大的缺点是其忽略了连续状态之间的关系。实际过程中，一个状态的效用值是由reward和下一个状态的期望效用值共同决定的，而这种直接计算效用值的方法是遵循bellman公式，通过概率转换模型和reward在状态空间中搜索状态效用值，并不能让agent实质地学习。在非常大的状态空间中这种方法会收敛的非常缓慢。

Passive ADP adptive dynamic programming algorithm

ADP使用dynamic programming的方法解决MDP问题

Passive ADP 使用bellman更新函数更新效用值

\[ U_{i}(s)=\sum_{s^{\prime}} P\left(s^{\prime} \mid s, \pi_{i}(s)\right)\left[R\left(s, \pi_{i}(s), s^{\prime}\right)+\gamma U_{i}\left(s^{\prime}\right)\right] \]

ADP 的使用条件是策略\(\pi\)是固定的，即到了某一个状态会做某个固定的动作，不固定的是转换模型P，passive ADP是通过增加trial的次数来不断修正transion model P，

Policy iteration algorithm

其中unchanged 是一个退出循环flag，一直到unchanged为true的时候退出repeat循环，该算法使用Q值作为状态值

policy iteration就是从一个初始策略\(\pi_0(s)\)开始，不断地对策略进行评估和迭代改进，一直到产生的所有的状态的状态值都不再改变，此处\(\pi_{x}\)的下标表示执行次数，如果换做是方格游戏的话则需要从某个状态开始，对所有状态都迭代多次后效用值才能够收敛。

总的来说分两步：

1. Policy evaluation: 策略评估，将使用动作\(\pi_i\) 的状态值\(U^{\pi_i}\)当成\(U_i\)，即\(U_i = U^{\pi_i}\)，其中\(\pi_i\)是在状态\(i\)上要被执行的动作策略（即计算一次所有状态在策略\(\pi_i\)下的下一步的状态值并当作当前状态的状态值）
2. Policy improvement: 计算一个新的，基于策略\(\pi_{i+1}\) 的MEU最大期望状态值，即基于\(U_i\)提前计算下一步所有状态的状态值

Passive TD learning algorithm

TD 效用值更新函数

\[ U^{\pi}(s) \leftarrow U^{\pi}(s)+\alpha\left[R\left(s, \pi(s), s^{\prime}\right)+\gamma U^{\pi}\left(s^{\prime}\right)-U^{\pi}(s)\right] \]

• \(\alpha\)是学习因子
• \(s'\)是观察到的下一状态，因此\(U^\pi(s')\)是对下一状态的估算效用值
• TD 更新函数和19章的权值更新有异曲同工之妙 \(w_{i} \leftarrow w_{i} + \alpha \sum_{j}\left(y_{j}-h_{\mathbf{w}}\left(\mathbf{x}_ {j}\right)\right) \times x_{j, i}\)

Passive TD 和Passive ADP的区别：

1. ADP是基于转换模型来更新的，而且在状态更新中不断修正transition modal，而TD是不基于概率转换模型来进行效用值更新，TD是由环境直接提供连续状态间的联系。
2. TD 相比于ADP更加简单，对于每一次单独的观察采样消耗的算力更小，变化性更强，但总体收敛的也较慢
3. TD 和 ADP都进行对本地估算的效用值的不断调整，使估算值能够更加能够和其后续状态保持一致性，但TD的目标是和下一个状态保持一致，而ADP则是和后续所有的状态保持一致性。