Decision Trees决策树

使用Entropy计算率先分割哪个decision tree的分支

计算一个随机变量的不确定性使用熵，如果一个硬币投掷后头面朝上的概率为1的话，那这个硬币代表的随机变量的不确定性就为0，如果一个硬币有50%的概率投掷硬币头朝上，则其熵计算为：

熵的计算公式：单位为比特

信息增益 information gain

一颗决策树中的非叶子节点有split函数，用于将当前所输入的数据分到左子树或者右子树。我们希望每一个节点的split函数的性能最大化。这里的性能是指把两种不同的数据分开的能力，不涉及到算法的时间复杂度。但是，怎么去衡量一个split函数的性能呢？这里我们使用信息增益来衡量G。如果G越大，说明该节点的split函数将输入数据分成两份的性能越好。

---

版权声明：本文为CSDN博主「ChainingBlocks」的原创文章 原文链接：https://blog.csdn.net/liangyihuai/article/details/103206360

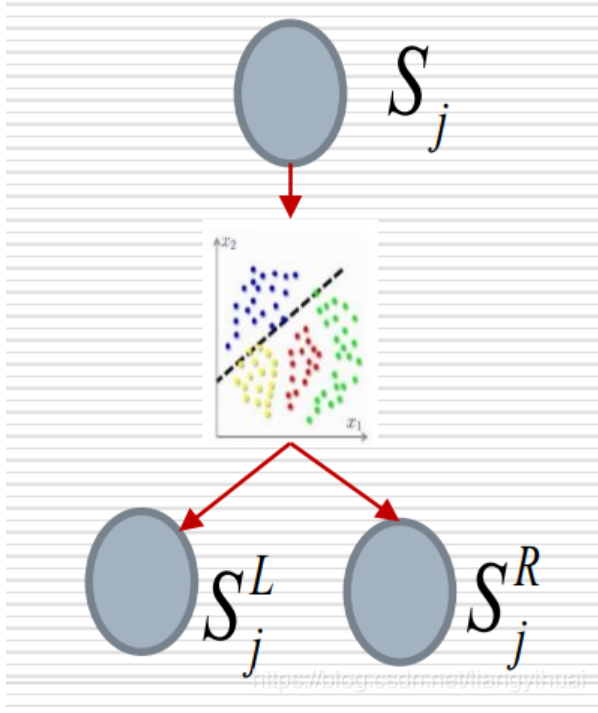
如果一个decision tree拥有不同的attribute将一个训练集分割成不同的组，每一组又分为正负两种不同的结果，可以通过这个attribute的information gain 来判断是否应该先对该组进行划分：

对于餐厅排队问题，可以通过顾客这个属性进行划分，而通过计算，对patrons划分的熵的reminder为

熵减去reminder就得到使用attribute A划分的information gain

通过对比使用type和使用patron的information gain

可以知道patrons的information gain要大于type,即使用patron节点,可以更好地将数据分割成一堆儿一堆儿的

使用chi-square来确定是否要对决策树进行剪枝

对于决策树而言,有些节点(状态)的数据是不相关的,即有可能会出现错误节点,这个时候需要将这些节点进行删除裁剪.

如何决定哪些节点需要被删减?在这个问题上,可以假设在统计上数据之间是没有相关性的,这个假设被称为Null hypothesis, 即数据之中没有浅在的一种模式及关联性. 要测试数据之间是否有关联性,则需要进行significance test, 即测试数据对完全没有关联性的偏离程度.

Significance test

对数据进行随机采样,如果随机采样的结果和标准分布的偏差非常接近(5%)以内,则意味着数据集之间就是没啥联系,就是说对这个数据集进行采样和自然状态下随机采样的结果是差不多的,数据之间的联系很微弱,没有什么明显的pattern.

通过对比k类占总samples数量的比例乘以总的正向sample的个数得到k类中正向sample的期望值,然后对比其期望值和实际k类中正/负类的sample的个数来看是否存在偏差.

比如一共有10类,100个samples,p有50个,n有50个

第5类中有p 3个,n 5个,则 那么和真实的 p 的偏差为 即存在关联性.

对于总体样本的偏差计算为:

对于, 如果数据毫无关联性,则 的值应该分布为 自由度的 chi-squared, 分布 ,不同的$$值则在不同的置信程度上驳斥数据的不相关性, 可以查表获得.

Chi-square test也是一种feature selection

Model selection 模型选择

数据集分成3种分别干不同的事情

1. training set: 训练集,用于训练出不同的模型
2. validation set:验证集,用于验证训练出来的备选模型,然后从诸多备选模型种挑出最好的一个
3. test set: 测试集,对最终模型进行测试

数据集不够时

交叉验证,即将数据集拆分成均等大小的k个,然后每一个分别轮换着作为一个训练集,剩余的作为测试集,分成几份就要多出来几倍的测试训练时间.

最极端的是把每一个数据都当做一个单独的训练集,成为LOOCV

为什么要用损失函数(loss function)而不是效用函数

1. 传统原因,使用最小化损失而不是最大化效用
2. 有些特殊场景,减少损失要好于增加效益,比如对垃圾邮件和正常邮件的分类,将垃圾邮件分类为非垃圾邮件的损失要远大于把非垃圾邮件分类成垃圾邮件的损失.

loss function 的定义: 使用输入预测的输出和真实的输出值的差值.

The loss function is defined as the amount of utility lost by predicting when the correct answer is :

损失:两个函数之间的差值的绝对值

损失:两个函数之间的差值的平方值

损失: 如果预测输出值和真实输出一样则 否则,适用于离散的输出值

: 附带概率分布的loss 模型,即假设输入输出是符合某种先验概率分布的,则模型的总loss可以计算为:

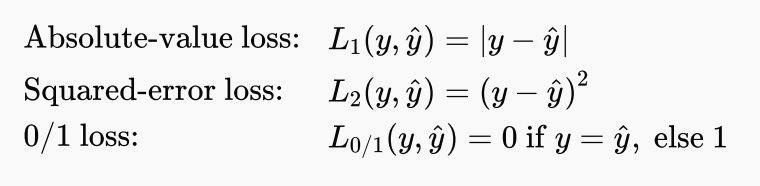
其中是样本和输出的先验概率,就是说输入的输出是的概率是,那么根据上式其总的loss就是样本的所有真实输出和预测值的差值的和.

:所有输出值和真实输出值的差值的加权平均

PAC 学习

监督学习的几个基本问题

• how many examples do we need to get a good h?
• What hypothesis space should we use?
• If the hypothesis space is very complex, can we even find the best or do we have to settle for a local maximum?
• How complex should be?
• How do we avoid overfitting?

对于需要多少个sample可以训练得到一个比较好的猜想hypothesis，可以如下思考。

1. 首先，如果我们规定一个错误率,如果训练集的错误率小于 的话则表明这个hypothesis是一个比较好的猜想，那么对于一个较好的Hypothesis来说，其本质上是围绕真正的预测函数形成的一个球，这个球的边界到真正的之间的距离是 ，所有好的对的猜想都应该在 以外 $$ 距离范围之内，并形成一个集合

2. 另外，所有不好的猜想 则相应的都应该存在于 以外 距离之外，并形成一个集合

3. 那么在我们去得到这个比较好的的时候，我们需要多少个样本去训练呢？我们可以从反面去思考，再训练的过程中：

   • 对于一个非常不好的hypothesis 的特征是其预测的样本结果的错误率要大于，即
   • 那么相反的，这个预测一个样本的正确率则为
   • 那么如果我们使用个样本去训练这个不好的Hypothesis ，并将其训练成一个能够正确预测个样本的Hypothesis的概率则为，即：

4. 那么对于不好的猜想集合，其包含一个能够预测N个样本并且都正确的猜想的概率：

5. 因为不好的猜想集合是所有猜想集合的子集，所以有：

   • 用表示一个极小数

6. 所以训练一个好的、且满足错误率小于$$的hypothesis所需要的样本数量为：

   • 上式称之为样本复杂度sample complexity

多元线性回归

猜想空间是一组有如下形式的函数

其中 是在方向向量上的截距，和其他的权值不同，因此可以使用一个定义为总是等于1的虚拟的特征输入(dummy input)。猜想可以用向量表示如下：

则最优的权值 矩阵是能够最小化样本损失平方差的那一个，即：

对于多元线性回归，其每一个特征权值的更新公式为：

使用差值矩阵形式，也是预测值和真实值之间的error，即损失函数：

求得（损失函数）的梯度为：

令梯度为0，可以求得：

可以得到所谓的normal equation：

过拟合问题

在高纬度空间，可能有于某些数据维度的特征在数值上恰巧拟合，但并不具备真正的关联关系，这种情况训练出来的hypothesis 存在过拟合问题，即只针对于某些数据集其预测能力很强，对于陌生数据表现很差。

解决过拟合问题主要使用正则化regularization的方法：

然后广义的损失函数就可以定义如下，即平均损失加上由参数 控制的hypothesis的复杂程度：

正则化的本质是最小化 ，等同于在 的限制下最小化 项，在这其中使用参数控制的取值大小。

正则化和正则化的对比，在有颜色的区域内，都是代表所取得值是小于的，椭圆形区域是损失函数的区域，菱形和圆形区域与椭圆区域相交的点，就是在小于值的的可行域中能取到满足损失函数的最小值。

由图可以看出，正则化不会取到0，而正则化有可能在处取值。