第二章

拉普拉斯矩阵

Jordan form matrix and transformation matrix

特征值 和右特征向量 满足

Theorem 2.1 L has rank N-1, i.e., is nonrepeated, if and only if graph G has a spanning tree

如果一个图G的拉普拉斯矩阵的秩是N-1，则 不重复的条件是 图G含有spanning tree，spanning tree是指该图有不只一个子树包含图中所有的顶点

且有以下推论：

1. 因为 所有的行自相加等于0，所以有

$$

$$

L c=0

$$

$$

其中, 是任意一个常数，这代表了每个矩阵必然含有特征值对应有特征向量,所以，即拉普拉斯矩阵的零空间里必含。

如果的维度是1，即拉普拉斯矩阵的秩为 ，则是该拉普来说矩阵无重复的特征值，且所对应的是其零空间内唯一的特征向量。

2. ⭐️拉普拉斯矩阵必然含有

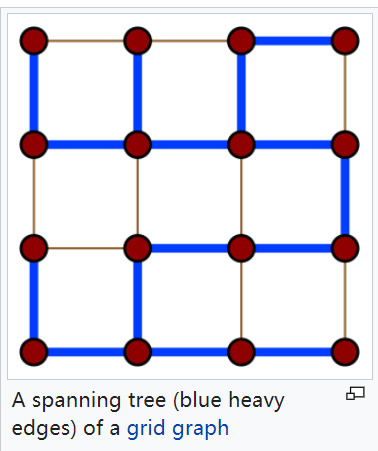
3. ⭐️如果图是强连接图，则图必有spanning tree且其拉普拉斯矩阵的秩为

4. ⭐️如果图有spanning tree，则

5. ⭐️如果图有spanning tree，则该图的拉不拉斯矩阵有一个无重复的特征值:，而且其他的特征值都有实数部分大于0

6. ⭐️所有的无向图都有对称的拉普拉斯矩阵，所以它们的图拉普拉斯矩阵的特征值都是实数

7. 拉普拉斯正则矩阵：用于两图比较特征值

Geršgorin Circle Criterion

Geršgorin Circle Criterion All eigenvalues of a matrix are located within the union of disks

矩阵E的所有特征值都在以对角线上元素为圆心，以每一行除掉对角线元素的加和绝对值为半径的圆的与集上面，对于拉普拉斯矩阵来说，每一个对角线元素都是该行其他节点的加和值乘以-1，则除去对角线元素，拥有最大加和绝对值得行是最大入度节点所在行，因为，每一行的disk都以该行对角线元素的度值为半径，为圆心的圆

The -th disk in the Geršgorin circle criterion is drawn with a center at the diagonal element and with a radius equal to the -th absolute row sum with the diagonal element deleted, . Therefore, the Geršgorin disks for the graph Laplacian matrix are centered at the in-degrees and have radius equal to .

临界稳定性

齐次连续线性时不变系统为临界稳定的充份必要条件是：系统传递函数中每个极点的实部都为非正值，且其中有一个或多个极点实部为零，且均为相异的单根，而其他的极点实部为负值。若所有的极点实部都是负值，系统渐近稳定，若有极点实部为正，则系统不稳定。

若系统是以状态空间来表示，可以推导其若尔当标准型，再分析是否临界稳定：系统临界稳定当且仅当其对于实部为0的若尔当区块为标量。

费德勒特征值 The Fiedler Eigenvalue

费德勒特征值是是拉普拉斯矩阵的第二特征值 ，代表了图的几何连接性，对于确定在图上的动态系统的相互作用速度的有重要意义。

对于无向连接图：

:最小节点入度

：节点数

: 图中任意两点最远距离

: 图中节点入度加和，即

一个图的费德勒特征值大，则在图上的动态系统达到稳态的时间就越短，即图中连接越多，任意两顶点间最远距离越短，则越容易达到稳态

单积分器共识动力学

在图上个节点，考虑节点的控制有单一积分器的控制器设计：

其中是该点对邻居节点的边权重

对于所有节点则有

于是发现单一积分器的一致性就与图拉普拉斯矩阵有密切关系

作为系统矩阵而言，其所有特征值都在复空间左平面，原因是拉普拉斯矩阵的特征值全部在右平面上，所以在左边，因此系统最终都是收敛稳定的，但有可能是不同的稳定方式。

于是，在系统平衡态的时候有：

因此全局的steady-state都存在于的零空间里，也就是说，只要找到的零空间的特征向量，就找到了该系统的稳态解。

如果的秩是 ,则矢量是其唯一的零空间解，所以有 :

其中是常数，且对于初阶系统而言，这个稳态的共识值为：

定理2.2 初阶系统共识收敛

本地投票协议使系统保证收敛的充分必要条件是该系统所在的图有旋转树(spanning tree)，共识值是公式（15）

Consensus for First-order Systems The local voting protocolguarantees consensus of the single-integrator dynamics if and only if the graph has a spanning tree. Then, all node states come to the same steady-state values The consensus value is given by (15)

证明：

对于，其解为：

如果图有旋转树，则除了以外，拉普拉斯矩阵 其他的特征值都在右复平面，所以对于系统来说，所有的特征值都在零点和左平面，即系统是marginally stable的，于是当时有：

取，,正则化使得，则有，然后有解：

其中第二项就是系统趋于稳定时得共识值，而第一项则代表了收敛速度，在时，第一项就变为定值，往后时刻只会比该值小，所以当时，逼近稳态值$ {i=1}^{N} p {i} x_ {i}(0) =c $

对于在图上使用低阶控制器运动的动态系统而言：

1. 节点状态收敛到一致的速度快慢大致取决于Fiedler特征值的大小

所有节点同步到初始态的平均值时第一特征向量即为稳态值

当所有节点都同步到初始状态节点的平均值时，也就是稳态时：

因为在稳态时，$ w^T_1x(0)={i=1}^{N} p {i} x_ {i}(0) = c=c$

即可以得到：

即

因为在无向图中，

所以有：

综上可以得出结论，稳态值为初始状态平均值的初阶系统，其拉普拉斯矩阵的第一特质值所对应的特征向量，就是其稳态值。

consensus leader

1. consensus leader定义为图中spinning tree的根节点
2. 所有节点都会向着leader节点状态进行同步
3. 拉普拉斯矩阵第一特征值对应的特征向量，其大于零的部分对应的节点就是leader节点
4. 一个图中可以有多个leader，但是最后同步状态不知道超哪个leader去，或者是朝着leader的平均值去？

Discrete--time dynamics

对于离散时间的单个节点而言，其运动有如下动力学

分布式本地控制器

closed-loop system

global input

global dynamics

Perron matrix

有所有特征值都在单位圈内的充要条件是：

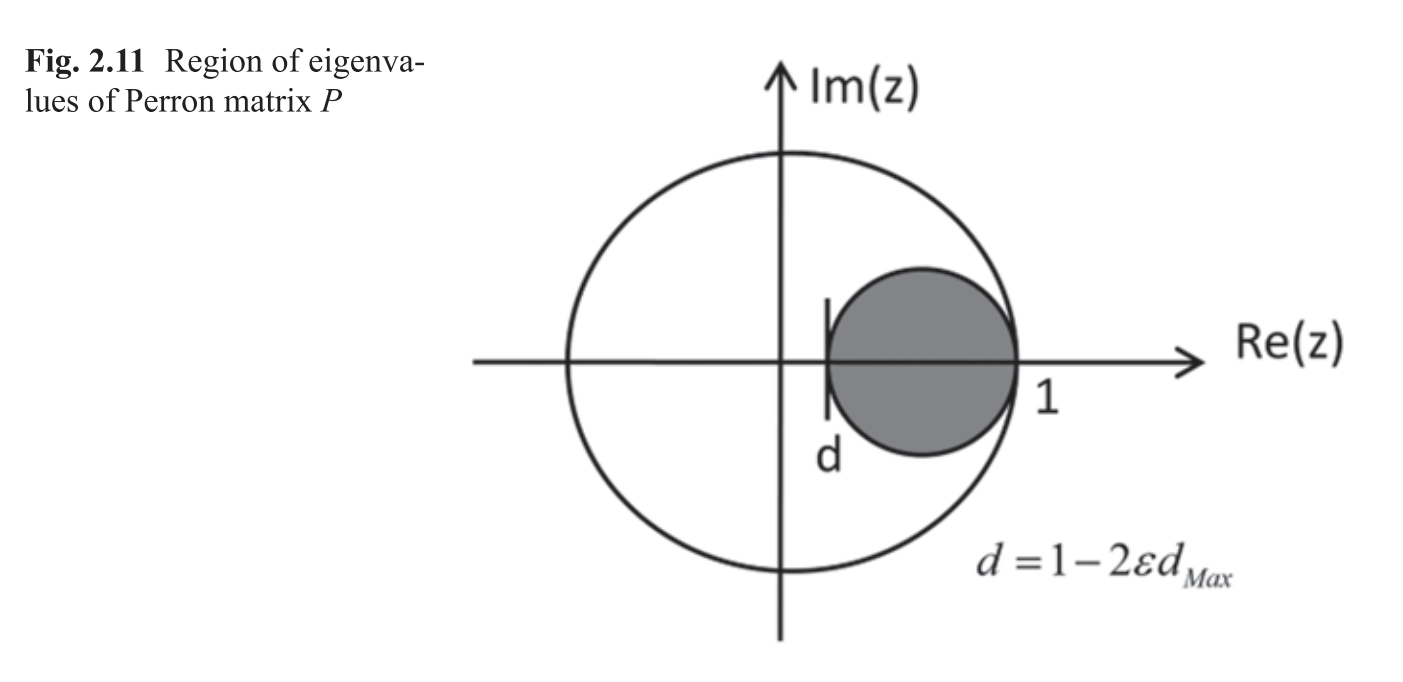
因为拉普拉斯矩阵的row sum是0，所以Perron matrix 的row sum是1，所以是perron matrix 的右特征向量，对应于特征值.

在稳态的时候，离散系统的稳态状态：

如果系统图有spinning tree，则，可以得出，则系统中所有节点的值都达到稳态时共识值，即

也就是对应在的

因为有spinning tree，所以公式（19）可用，即:

所以（28）等于：

所以前一个状态等于后一个状态，所有时刻的状态和左特征向量的矩阵乘积都相等，即共识值为一个定值：

本地控制协议

其中是节点i的入度。

离散时间下的节点动力学：

相应的全局控制：

全局动力学为：

矩阵 为正则化共识矩阵

对于F矩阵，如果图有spinning tree，则有如下性质：

1. F矩阵有简单特征值
2. 初以外其他特征值都在零点圆心单位圆内
3. 系统是临界稳定的，状态趋于稳态值
5. 是的第一特征值对应的右特征向量
6. 所有特征值都在下图中灰色区域

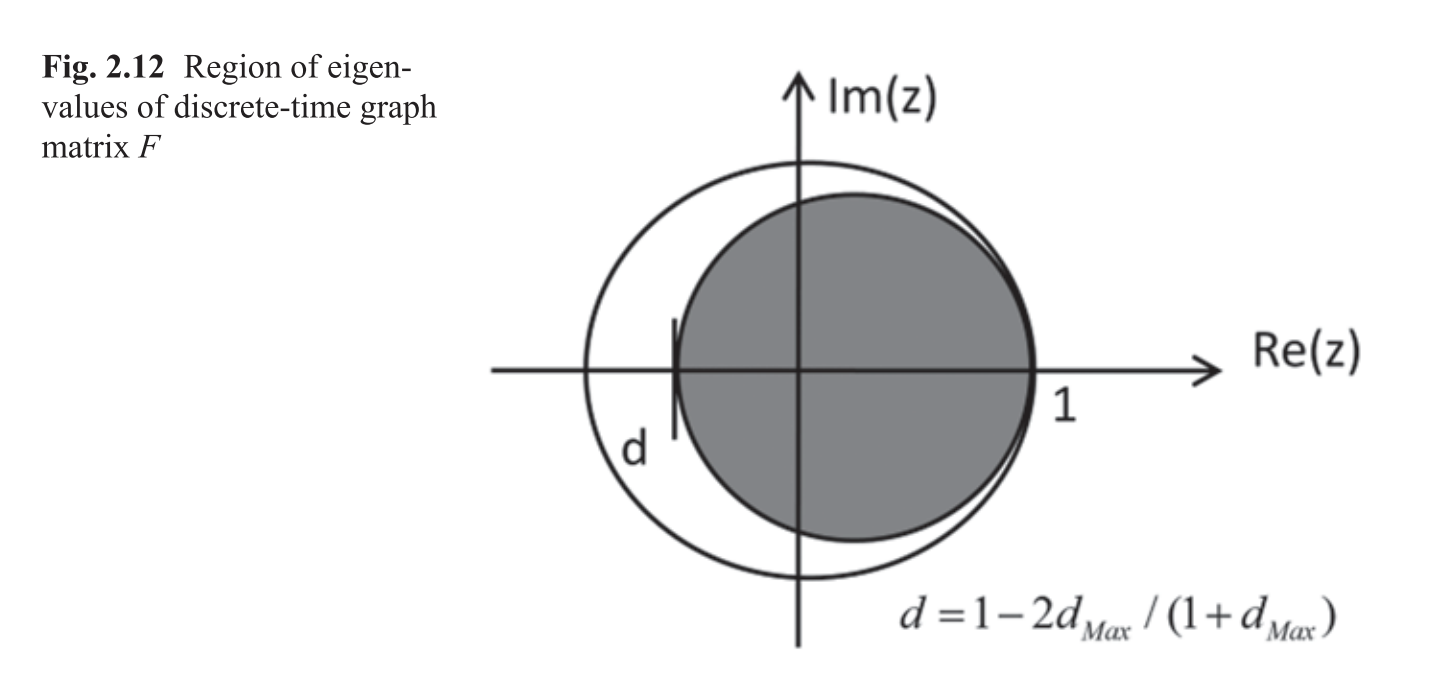
其中左特征向量 对应 特征值

和上一个分布式protocol相似，共识值是一个运动常量，即：，不同的是分布式协议中是矩阵Perron matrix 的第一左特征向量，而这里是共识矩阵 的第一左特征向量。但是由于矩阵中第 i 行除以了，所以导致图是不平衡的，所以尽管图是平衡的，也不能达到所谓的平均共识，即以初始态平均值为共识值得稳态。但是如果所有的节点都有相同入度，则在平衡图上可以达到平均共识，因为是相同的，这种情况称之为d-regular.