PCA分析

Eigenface

PCA有很多作用，比如在人脸识别领域，拾取人脸得关键特征。最著名的一个例子是所谓的eigenface。

顾名思义，eigenface就是脸的eigenvalue，即脸的特征（其实任意图片都有特征，但是使用一类图片比如人脸图片较为好比较）。

使用PCA提取人脸图片的特征，并且将其重新组成图片，过程如下。

  1. 获取张同一个人不同的人脸照片，比如192x168像素的照片，用灰度表示（比较简单，这样每一个pixel就只有一个值而不是3个值了）。
  2. 将每一张照片变成列向量，每一列代表一个照片，构成一个矩阵，即矩阵的维度是。
  3. 计算矩阵的每一行的平均值，得到一个 的列向量，然后将这个列向量扩充成矩阵，变成 的矩阵，每一列的值都相同，这个矩阵称之为均值矩阵 。
  4. 通过公式算出去平均值后的矩阵
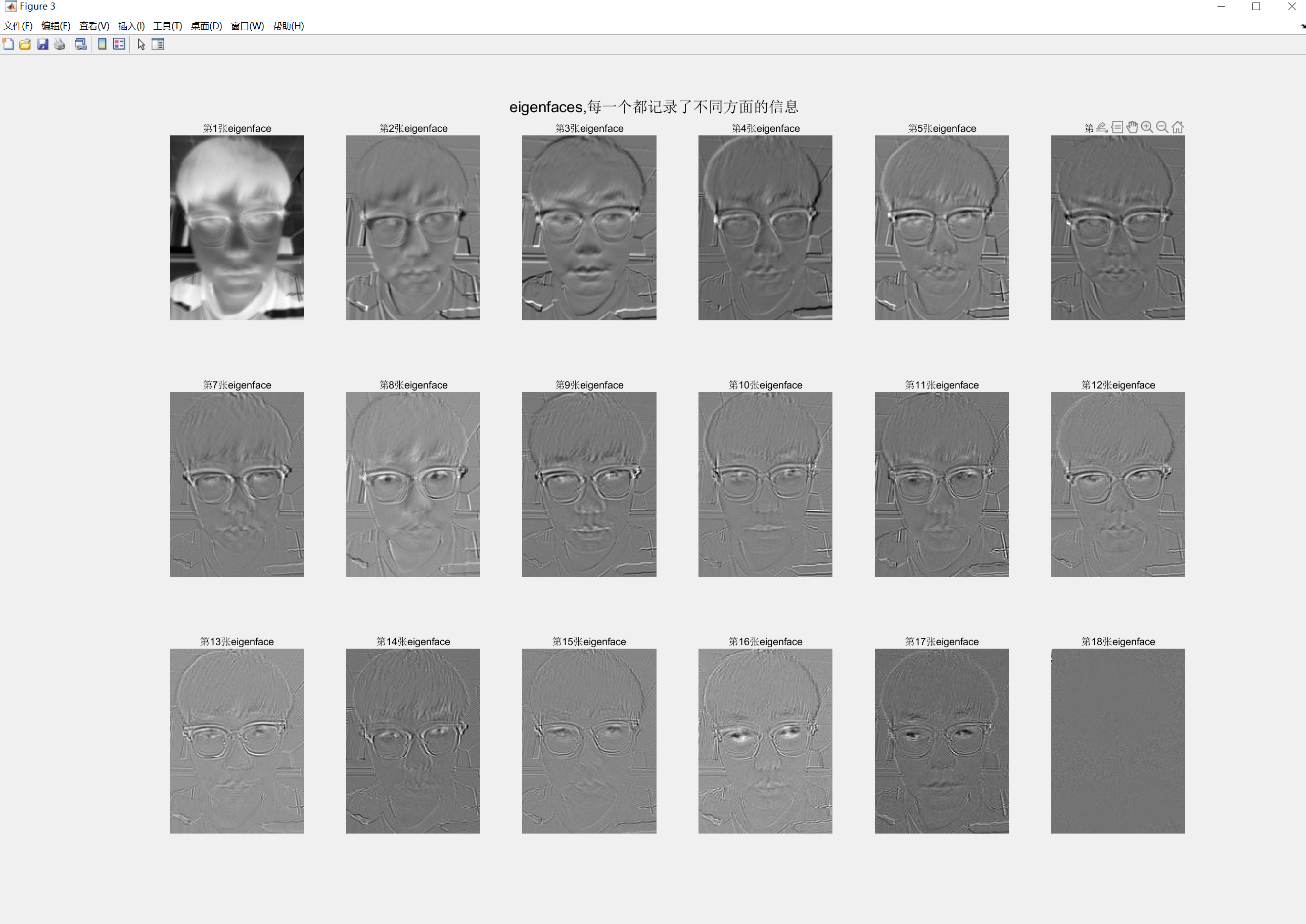
  5. 将进行SVD分解得到 其中，矩阵就是eigenface矩阵，每一列就是每张照片的eigenface,每一张都记录了不同方面的信息

以上五步就可以的出来eigenface，下面发一个代码，以及本人靓照：

image-20210515230156788

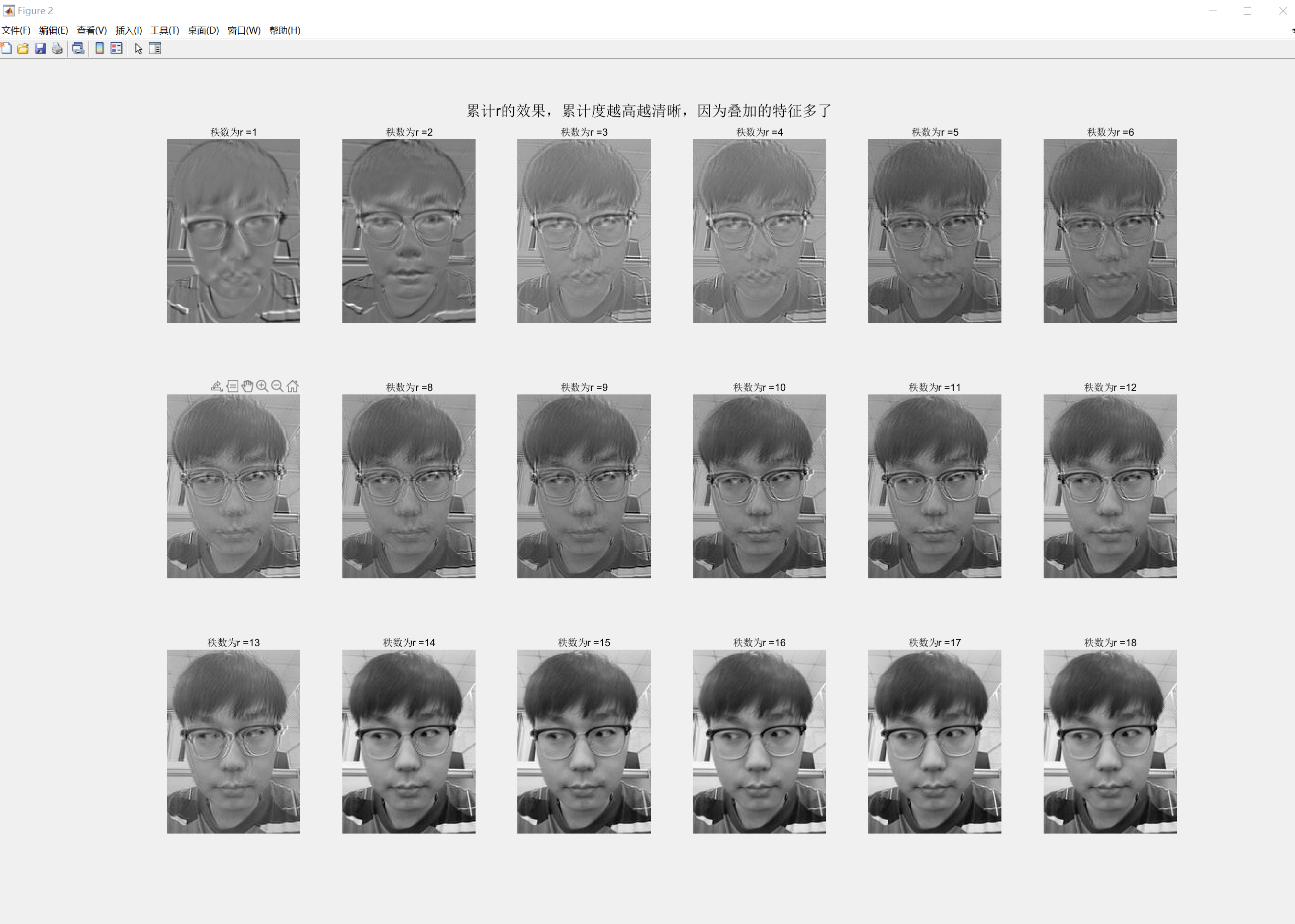
使用eigenfaces可以拟合出来原图，选取秩数的不同会得到不同的还原度，而且即便用于测试的图片非常不一样，下图我用了一张类似的照片做测试。

注意上图最后一张，也许是使用了matlab的svd(,'econ')命令导致的，最后一张的图像总会得到类似于马赛克的效果。

image-20210515230330673

图片原图：

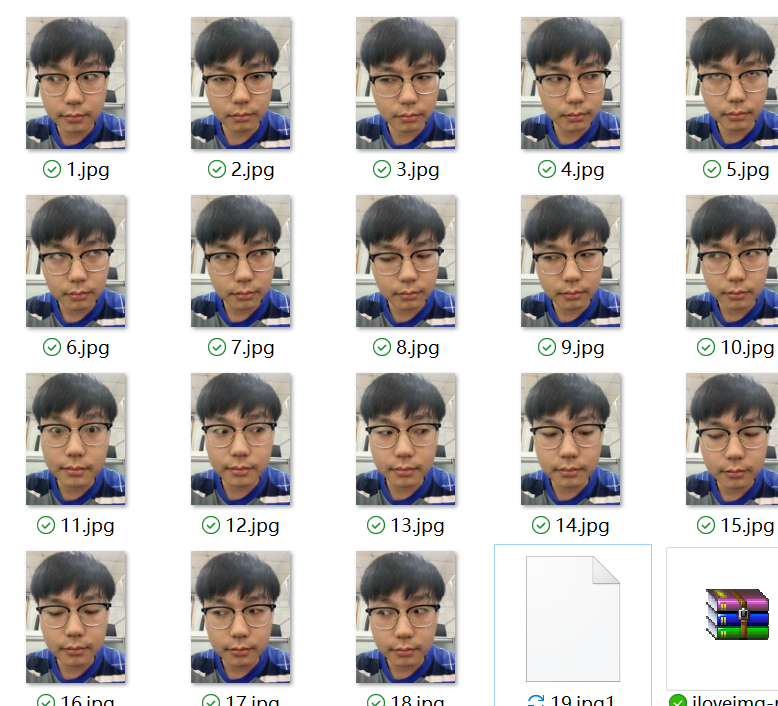
image-20210515231724032

我用于测试的图片：

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
clear all, close all, clc

file_path = 'D:\OneDrive\西安交大\实验\MATLAB 练习\Data-driven Science\Practice\svd\myface\eyes\';
h = 192; % 高
w = 144; % 宽
n = length(dir(strcat(file_path,'*.jpg'))); %图片数量
m = h*w; % 单列维度
I = zeros(m,n);
for i=1:n-1
    img = strcat(num2str(i),'.jpg');
    gray_img = rgb2gray(imread(strcat(file_path,img)));
    I(:,i) = reshape(gray_img,m,1);    %将所有的像素变成列向量
%     imagesc(reshape(I(:,i),h,w)); %展示图片
%     pause(0.1)
end
%% 搞出来平均脸然后去平均后进行SVD
avg_face = mean(I,2);
% imagesc(reshape(avg_face,h,w)), colormap gray; %平均脸
%画出所有的eigenface，越往后占的重要程度越低，到最后一张变成一坨糊糊
B = I-avg_face*ones(1,size(I,2));
[U,S,V] = svd(B,'econ');
for i = 1:n
    imagesc(reshape(U(:,i),h,w));
    pause(0.1);
end

%% 画出不同r的eigenface，用最后一张照片做测试
test_img = reshape(rgb2gray(im2double(imread(strcat(file_path,strcat(num2str(n),'.jpg'))))),m,1); 
truncated = test_img - avg_face;

% for r = 1: 1 :n
%     new_img = avg_face + (U(:,1:r)*(U(:,1:r)'*truncated));
%     imagesc(reshape(new_img,h,w)),colormap gray;
%     pause(0.1)
% end

%% 将所有图画到一张上去，一定注意不要太多张图
f=figure;
row = 3; %3 行排列
col = floor(n/row); 
zoom = 2;% 缩放最后一张图的大小
set(gcf,'Position',[500 500 col*w*zoom row*h*zoom])
movegui(f,'center');

for r = 1:n
    new_img = avg_face + (U(:,1:r)*(U(:,1:r)'*truncated));
    subplot(row,col,r),imagesc(reshape(new_img,h,w));colormap gray, axis off;
    s = sprintf('%s%d','秩数为r =',r);
    title(s);
end
sgtitle('累计r的效果，累计度越高越清晰，因为叠加的特征多了');

eigenfaces = figure();
set(gcf,'Position',[200 500 col*w*zoom row*h*zoom])
for i=1:n
    subplot(row,col,i),imagesc(reshape(U(:,i),h,w));colormap gray, axis off;
    s = sprintf('%s%d%s','第',i,'张eigenface');
    title(s);
end
sgtitle('eigenfaces,每一个都记录了不同方面的信息');

帅的人都很细心地发现了上面的图片都只动了我的慧眼，其他部分保持了不变，这是因为SVD对于图片处理有天然的缺陷。即SVD 对图像进行分析的时候受到图像的排放方式影响很大。

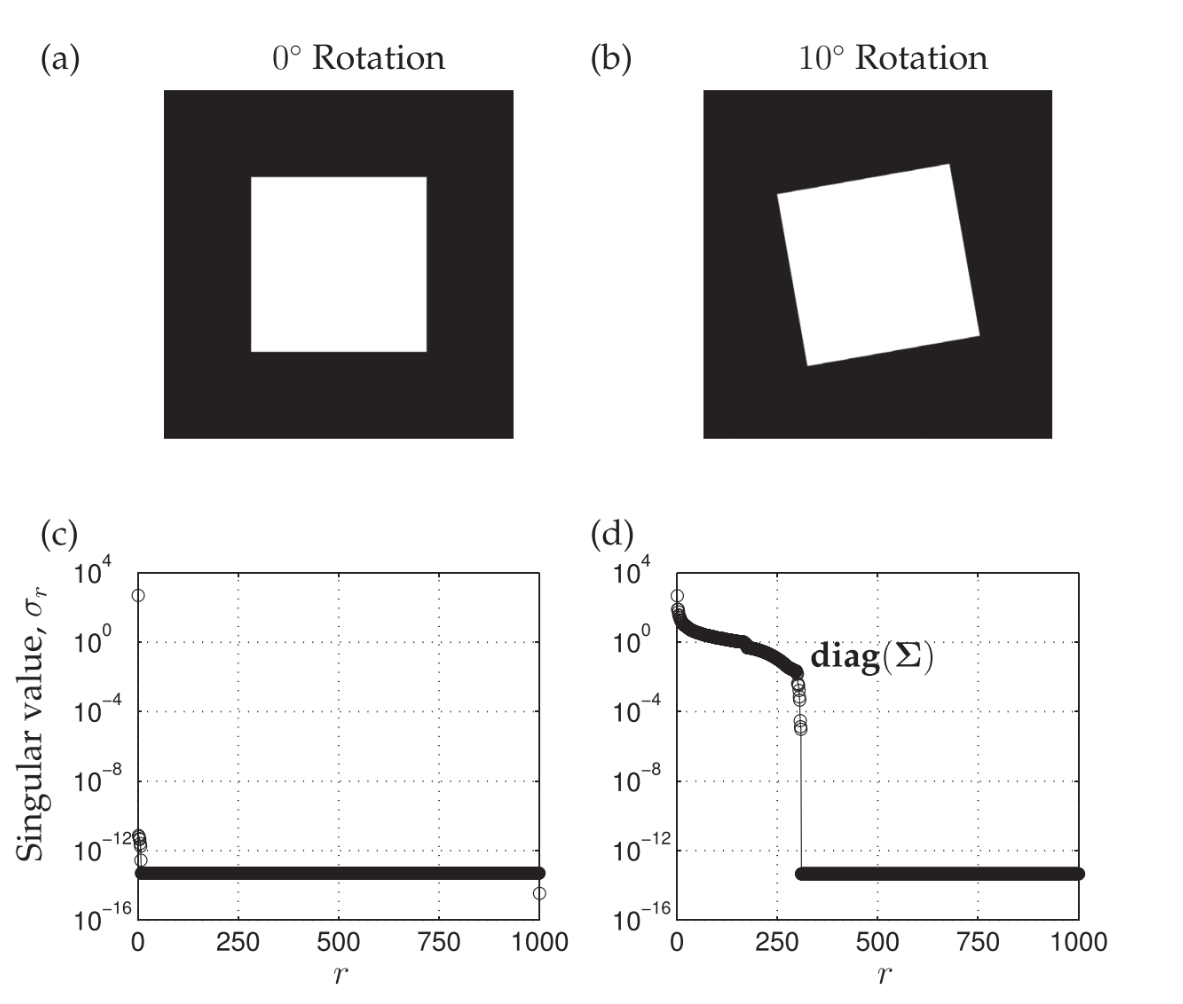
image-20210515232054145

图片来源于:

SVD受到图像内主体的排列方位影响很大，因为这直接导致了整个图像矩阵奇异值改变。而奇异值分解是对图像进行操作的主要办法，通过获取不同程度的秩的图像，可以得到不同还原度的原图像。

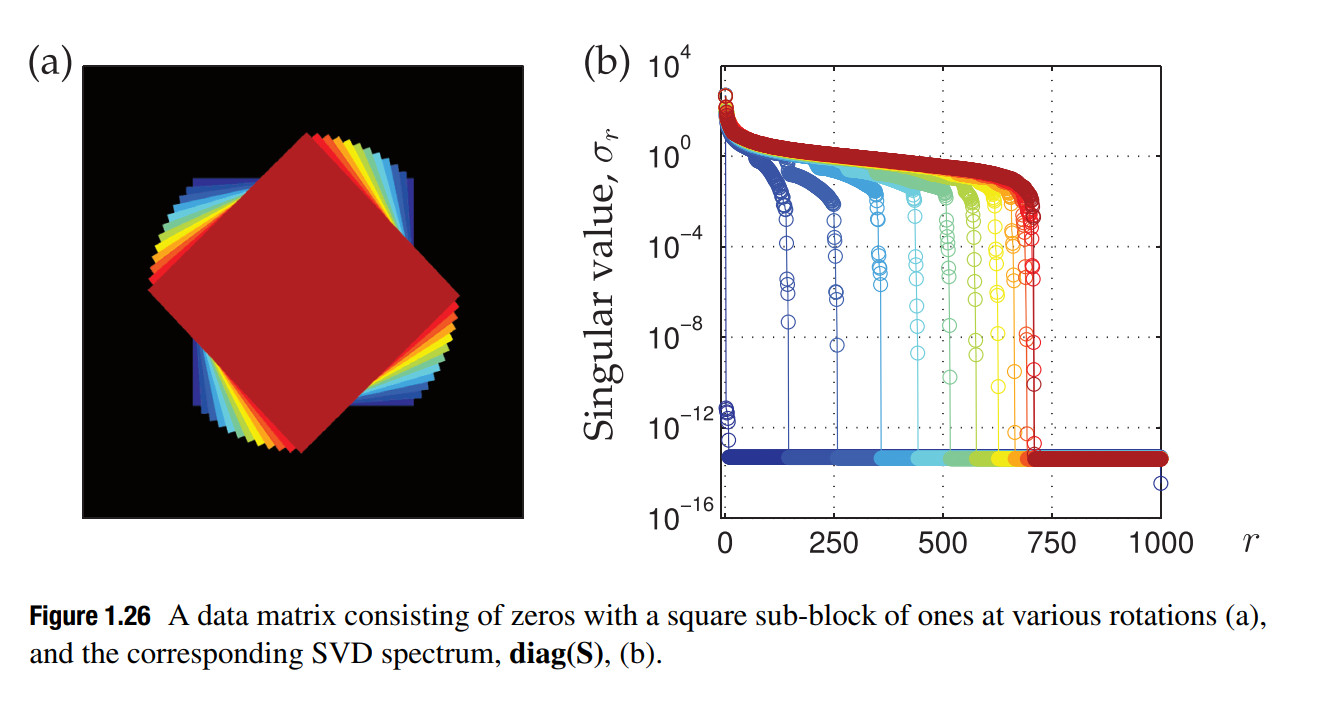
image-20210510212308716

如何选取最优秩r作为分界线实现图片压缩

对于使用SVD方法对图像进行压缩，其实实质上是我们不需要将所有的奇异值都给弄出来用作压缩图片使用，因为奇异值和奇异向量是按照其重要程度排序的，而且其奇异值矩阵中，前面一小部分奇异值的重要性是是超过后面大部分奇异值重要性之和的。因此，在压缩图像的时候，我们只需要前面 个奇异值和奇异向量就可以实现图像的压缩。

image-20210515185449092

硬分界线r

我们设法搞一个分界线，这个分界线以使用奇异值矩阵秩的数量为边界，使其能够保留90%以上信息的前提下实现使用最小秩的数量，也就是使最小。这个分界线就是下图中如何划分和的关键。

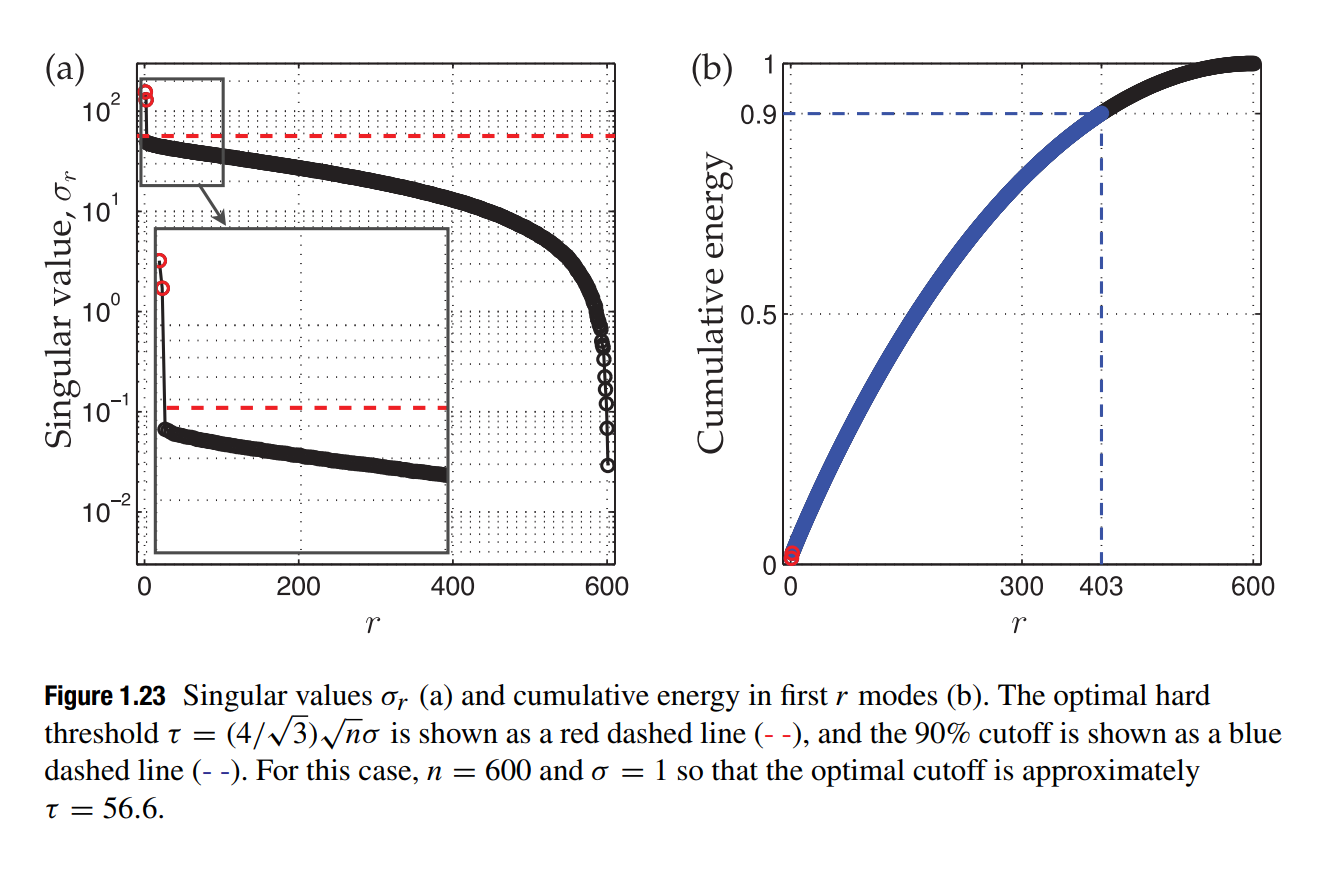
有一种方法是最优硬分界线，选取秩r大于该分界线的部分最为Truncated SVD，往往最有效率。

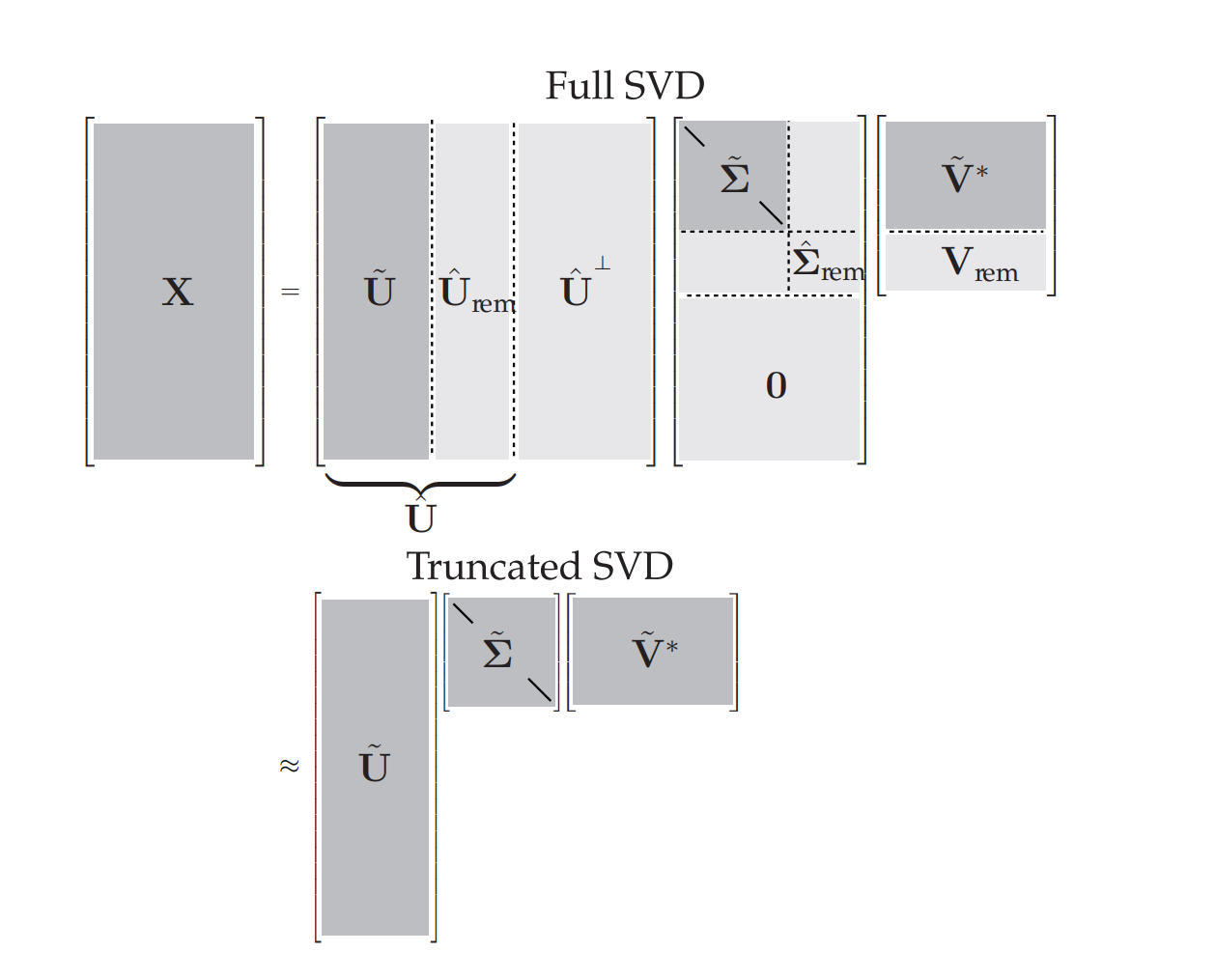
fullsvd2truncatedsvd

那么最优硬分界线划分假设被分解的矩阵可以被分成两个部分： 其中 是高斯噪音，是噪音的magnitude。

  1. 如果,即是个方阵，而且$已知则硬分界线为：$

  2. 如果,且 即是个非常细长的矩阵，则替换成 ：

  3. 如果,而且$未知，则最优硬分界线为：$

    其中是奇异值的中位数, 由下式解出：

例子：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
clear all, close all, clc
%% 造出来一个真实X
t = (-3:.01:3)';
Utrue = [cos(17*t).*exp(-t.^2) sin(11*t)];
Strue = [2 0; 0 .5];
Vtrue = [sin(5*t).*exp(-t.^2) cos(13*t)];
X = Utrue*Strue*Vtrue';
figure, imshow(X);
%% 加噪音
sigma = 1;
Xnoisy = X+sigma*randn(size(X));
figure, imshow(Xnoisy);
%% 使用硬分界线产生一个clean matrix
[U,S,V] = svd(Xnoisy);
N = size(Xnoisy,1);
cutoff = (4/sqrt(3))*sqrt(N)*sigma; % Hard threshold
r = max(find(diag(S)>cutoff)); % Keep modes w/ sig > cutoff
Xclean = U(:,1:r)*S(1:r,1:r)*V(:,1:r)';
figure, imshow(Xclean)
%% 找到90%累计能量
cdS = cumsum(diag(S))./sum(diag(S));  % Cumulative energy
r90 = min(find(cdS>0.90));  % Find r to capture 90% energy
X90 = U(:,1:r90)*S(1:r90,1:r90)*V(:,1:r90)';
figure, imshow(X90)

%% plot singular values 画图
semilogy(diag(S),'-ok','LineWidth',1.5), hold on, grid on
semilogy(diag(S(1:r,1:r)),'or','LineWidth',1.5)
plot([-20 N+20],[cutoff cutoff],'r--','LineWidth',2)
axis([-10 610 .003 300])
rectangle('Position',[-5,20,100,200],'LineWidth',2,'LineStyle','--')
     
figure
semilogy(diag(S),'-ok','LineWidth',1.5)
hold on, grid on
semilogy(diag(S(1:r,1:r)),'or','LineWidth',1.5)
plot([-20 N+20],[cutoff cutoff],'r--','LineWidth',2)
axis([-5 100 20 200])
     
figure
plot(cdS,'-ok','LineWidth',1.5)
hold on, grid on
plot(cdS(1:r90),'ob','LineWidth',1.5)
plot(cdS(1:r),'or','LineWidth',1.5)
set(gca,'XTick',[0 300 r90 600],'YTick',[0 .5 0.9 1.0])
xlim([-10 610])
plot([r90 r90 -10],[0 0.9 0.9],'b--','LineWidth',1.5)

image-20210510211312407
image-20210510211636298