SVD奇异值分解

Sheldon Zheng2021-05-132022-11-12

SVD 使用 correlations 方法计算

首先在说SVD之前回忆一波特征值分解：

特征值分解

特征值分解简单来说就是把矩阵分解成特征向量矩阵特征值形成的对角矩阵特征向量矩阵的逆的形式,即其中是的特征向量

上式还可以写成这样，即原矩阵特征向量矩阵 = 特征向量矩阵特征值矩阵，特征值分解只能应用于方阵

SVD分解

关于一个向量 ,首先将其看成是列向量的矩阵,且假设 $，（）$

则是一个的矩阵

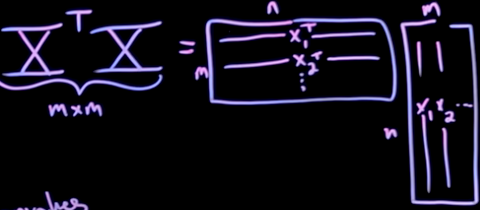
而这个矩阵就是矩阵中相互之间的相关性。

解释完的含义就可以看SVD分解了

首先SVD的分解形式为：

其中称之为的左奇异向量矩阵，称之为的奇异向量矩阵，和都是共轭转置矩阵，即其本身乘以其共轭转置得到单位矩阵。

$，$

$、$ 如果不是复数矩阵。

称之为的奇异值矩阵，其中是对角矩阵，且每个奇异值的重要性按行顺序排列。

SVD分解可以是非方阵，也就是说任何矩阵都有其奇异值矩阵、左/右奇异向量矩阵，这和特征值分解是不同的。

SVD分解和特征值分解的关系

对和进行简化SVD分解可以分别得到

注：所谓简化SVD分解是matlab的一个函数svd（X,'economy'），其得到的是近似最优，以的维度确定的维度，下面将矩阵加帽以表示

则可以写成：

上面两个式子，结合公式可以推理得到的是和都是上述对应矩阵和的特征向量矩阵，而是特征值。也就是说，一个矩阵和其自身转置相乘得到其协方差阵，然后进行协方差特征值分解，得到的是的右特征值，得到的是左特征值，这样便实现了使用特征值分解得到奇异分解的结果了。

但是需要注意的是在公式中得出来的的矩阵一般来说都非常巨大，是维矩阵，所以应该尽量避免（一般情况下数据集行大于列，尤其是使用了Matlab命令svd(A,'economy')的时候）。

使用snapshot的方法进行左singular vector的计算

当使用的时候，我们可以获取 $、$ 的值，这个时候我们可以求出的值为：这个方法就是snpshot，因为矩阵就相当于在时间序列上的变换，每一列（的每一行）相当于一个时间点所有的数据的融合。

Underdetermined system 和overdetermined system

两种系统，用

表示的话，大概是这个样子：

对于第一种不确定系统，其系统矩阵的形状如下：

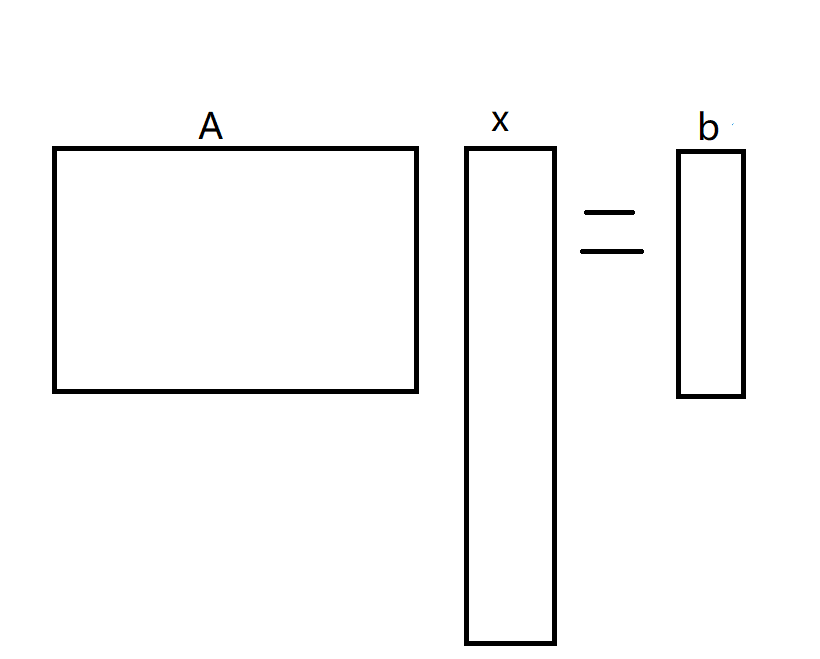
这种情况下，因为的数量众多，无法提供足够的数量去填充，因此系统有无数个解，通俗用一个公式解释就是 ,对于 $、$ 有无穷多个解满足此公式，因为的数量只有一个而变量有两个。

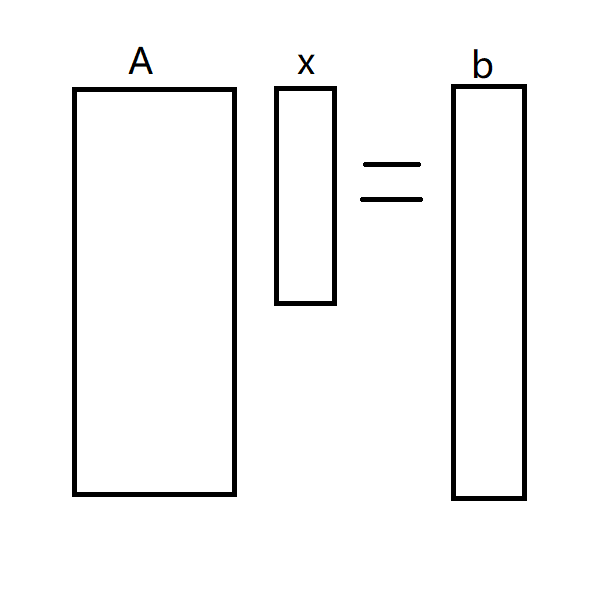
另一种情况就是 over determined system，这种情况就是变量过少，结果过多，导致没有一个准确的解。

基于SVD的PCA 分析

对以下视频的一个笔记，观看视频需要梯子。

PCA 算法

话不多说，先上如何计算PCA。

假设是一个矮胖矩阵：

首先对一个矩阵所有行进行的平均运算，得到一个很胖的单行向量，维度的矢量。

然后进行构建矩阵，用一个单位列向量构建： 2. 然后用减去得到去掉均值的矩阵：

计算的协方差矩阵：
计算协方差矩阵的特征值和特征向量：

其中是的第一个特征向量。是的特征向量矩阵

可以通过特征值分解（eigen-decomposition）进行解析：
其中是特征值，是特征向量
最后使用和的乘积求出principal components 其中称之为loadings

在此结果上，因为所以的出来principal components可以是：其中是的奇异值，是左奇异向量。

知识痛点补充：

为什么上述的协方差计算使用$ $而不是$ $作为系数？

首先明确协方差和方差的区别，数据的方差反映的是一个数据集自身的变化程度，也就是这个数据集的离散度，是对一个随机变量的测量值。

协方差则是描述对于不同的，相关的随机变量之间的变化关系，比如一个人的身高和体重两个变量的关系是正相关的，那么这两个变量的协方差就描述了身高和体重的变化之间的相互影响，就是多少身高带来多少体重、或者是多少体重的变化带来多少身高的变化。

因为在我们使用的任何数据集中，基本上都是更大一部分数据集的子集。在这部分数据集中，我们求得的协方差并不是能反映整体数据集的自然误差状态。换句话说，如果我们用做系数，就相当于我们用了大数据集中的一部分数据的协方差去反映整个大数据集的测量误差，所以用而非来弥补这种不合理性。比如我们在一个班里抽取学生的身高体重样本来反映整个班级的身高体重水平，班里有100个学生，我们现在取了20个学生（因为我们没有时间把100个学生的身高体重都测量一遍），使用他们的身高体重求协方差，然后用这个协方差去衡量整个班级的身高体重水平，这个时候我们的数据集只是这个大数据集的一小部分，所以我们的衡量是有偏差的，因此我们用而不是来抵消这种偏差。