SVD关键秩r分界线选取

截取关键成分

最优硬分界线

在SVD分解中，选取合适的秩r作为分界线至关重要。这个分界线就是下图中如何划分和的关键。有一种方法是最优硬分界线，选取秩r大于该分界线的部分最为Truncated SVD，往往最有效率。

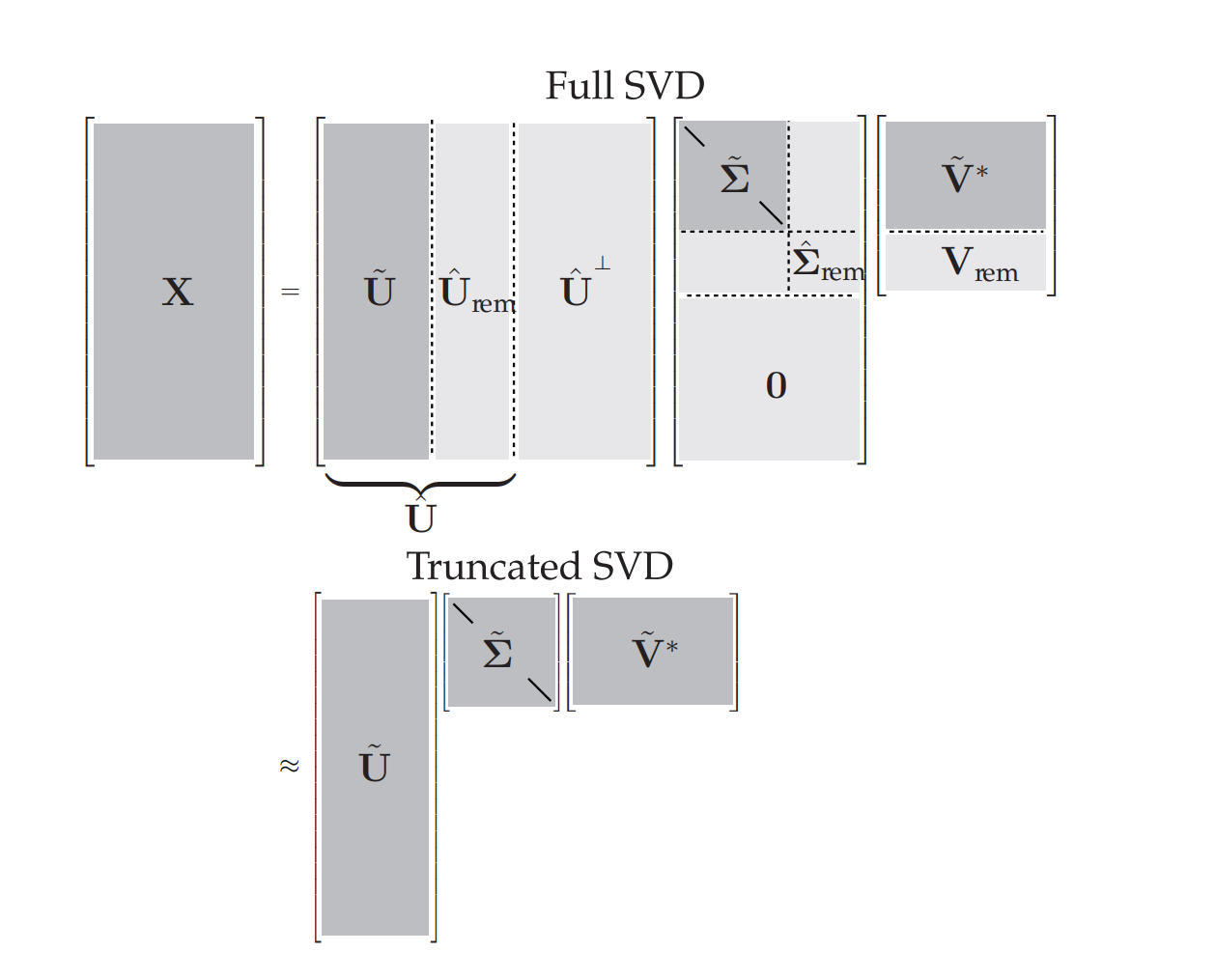
fullsvd2truncatedsvd

那么最优硬分界线划分假设被分解的矩阵可以被分成两个部分： 其中 是高斯噪音，是噪音的magnitude。

  1. 如果,即是个方阵，而且$已知则硬分界线为：$ $$

  2. 如果,且 即是个非常细长的矩阵，则替换成 ：

  3. 如果,而且$未知，则最优硬分界线为：$ $$

    其中是奇异值的中位数, 由下式解出：

    书中例子：

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    46
    47
    clear all, close all, clc
    %% 造出来一个真实X
    t = (-3:.01:3)';
    Utrue = [cos(17*t).*exp(-t.^2) sin(11*t)];
    Strue = [2 0; 0 .5];
    Vtrue = [sin(5*t).*exp(-t.^2) cos(13*t)];
    X = Utrue*Strue*Vtrue';
    figure, imshow(X);
    %% 加噪音
    sigma = 1;
    Xnoisy = X+sigma*randn(size(X));
    figure, imshow(Xnoisy);
    %% 使用硬分界线产生一个clean matrix
    [U,S,V] = svd(Xnoisy);
    N = size(Xnoisy,1);
    cutoff = (4/sqrt(3))*sqrt(N)*sigma; % Hard threshold
    r = max(find(diag(S)>cutoff)); % Keep modes w/ sig > cutoff
    Xclean = U(:,1:r)*S(1:r,1:r)*V(:,1:r)';
    figure, imshow(Xclean)
    %% 找到90%累计能量
    cdS = cumsum(diag(S))./sum(diag(S));  % Cumulative energy
    r90 = min(find(cdS>0.90));  % Find r to capture 90% energy
    X90 = U(:,1:r90)*S(1:r90,1:r90)*V(:,1:r90)';
    figure, imshow(X90)

    %% plot singular values 画图
    semilogy(diag(S),'-ok','LineWidth',1.5), hold on, grid on
    semilogy(diag(S(1:r,1:r)),'or','LineWidth',1.5)
    plot([-20 N+20],[cutoff cutoff],'r--','LineWidth',2)
    axis([-10 610 .003 300])
    rectangle('Position',[-5,20,100,200],'LineWidth',2,'LineStyle','--')
         
    figure
    semilogy(diag(S),'-ok','LineWidth',1.5)
    hold on, grid on
    semilogy(diag(S(1:r,1:r)),'or','LineWidth',1.5)
    plot([-20 N+20],[cutoff cutoff],'r--','LineWidth',2)
    axis([-5 100 20 200])
         
    figure
    plot(cdS,'-ok','LineWidth',1.5)
    hold on, grid on
    plot(cdS(1:r90),'ob','LineWidth',1.5)
    plot(cdS(1:r),'or','LineWidth',1.5)
    set(gca,'XTick',[0 300 r90 600],'YTick',[0 .5 0.9 1.0])
    xlim([-10 610])
    plot([r90 r90 -10],[0 0.9 0.9],'b--','LineWidth',1.5)
    image-20210510211312407
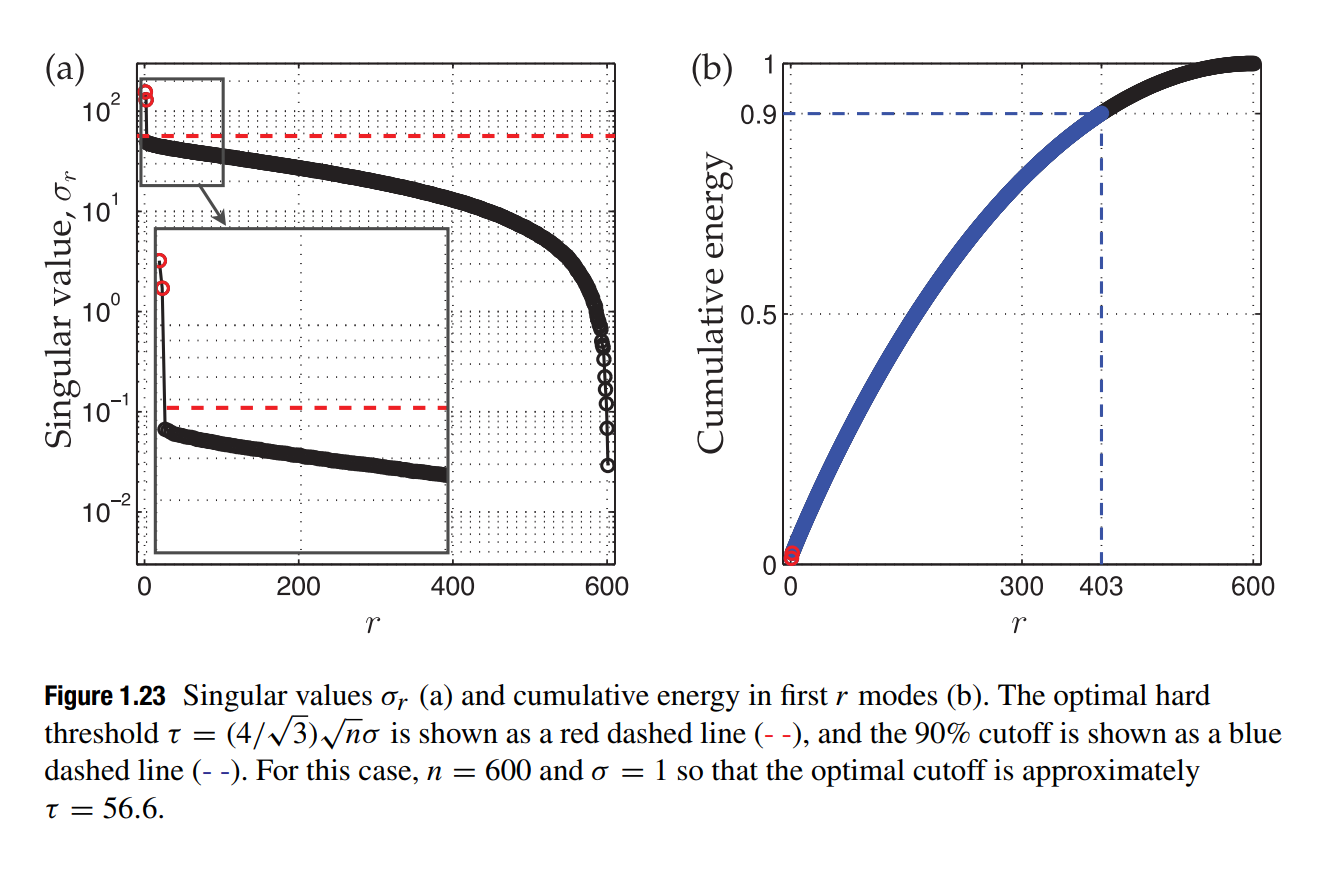
image-20210510211636298

SVD 的缺点

SVD 对图像进行分析的时候受到图像的排放方式影响很大

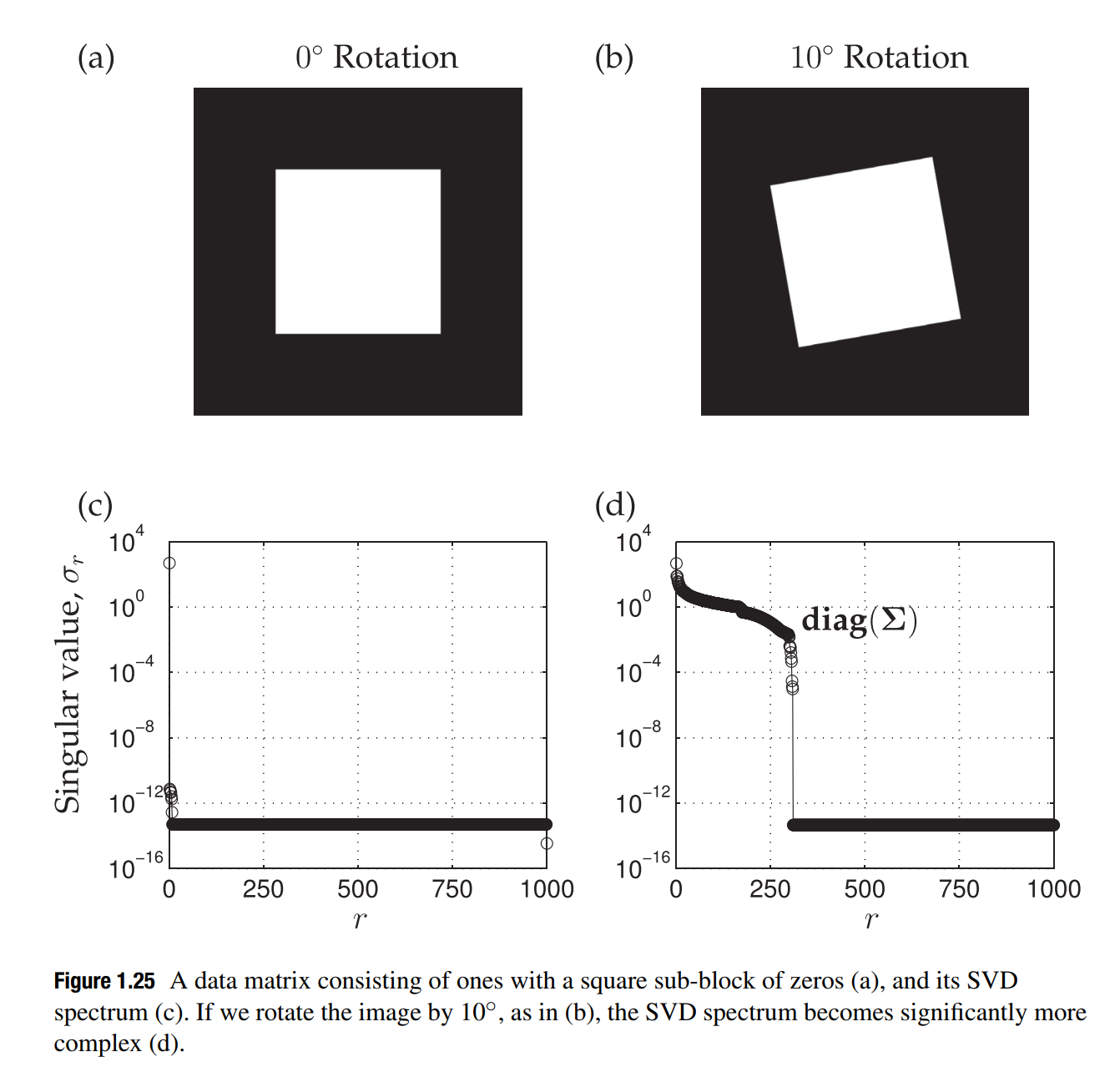
image-20210510212205987

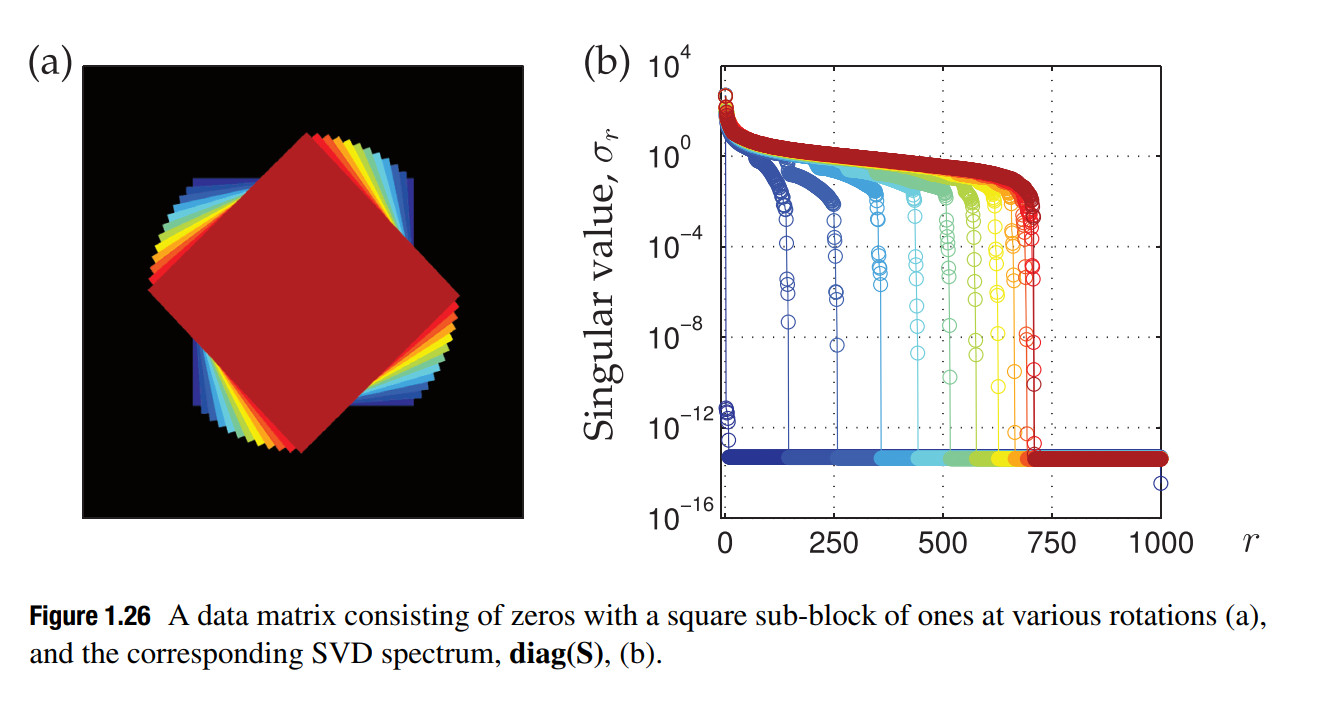
SVD受到图像内主体的排列方位影响很大，因为这直接导致了整个图像矩阵奇异值改变。而奇异值分解是对图像进行操作的主要办法，通过获取不同程度的秩的图像，可以得到不同还原度的原图像。

image-20210510212308716