使用SVD 奇异值分解进行regress回归

Truncated SVD

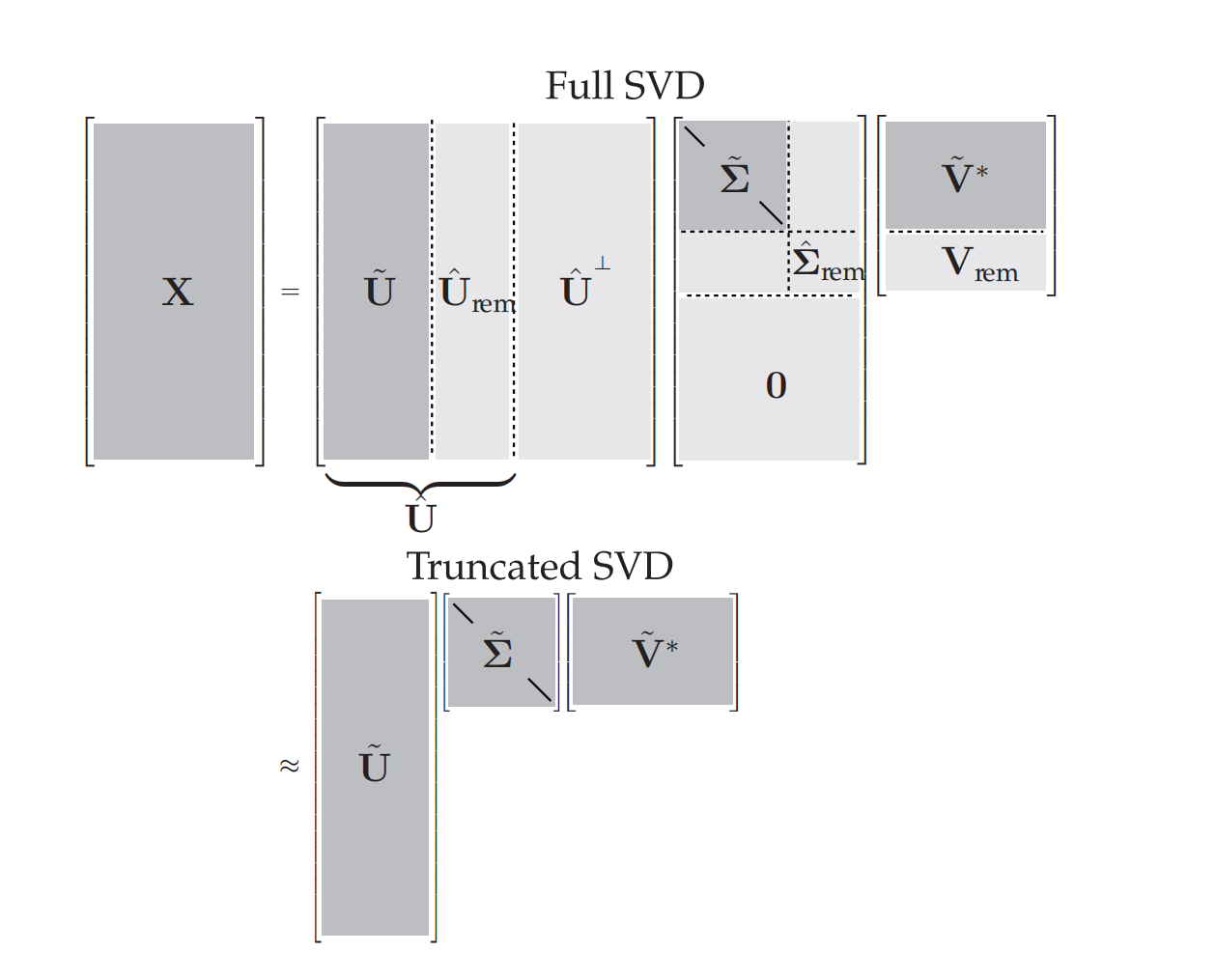
Truncated SVD见下图：

其中rem代表被截取后的剩余部分。

对于矩阵而言，我们将其分解为 的形式，其中，和都是酉矩阵，即其与自身的共轭转置相乘等于单位矩阵的矩阵（）。

则是一个对角矩阵，对角线上的值都是矩阵的特征值。

这样对一个矩阵分解就叫做SVD分解（singular value decomposition）。

对于而言，如果矩阵并不是全秩的矩阵(意思是其所有的行或列并不是都不相关的 not independently related)，矩阵的秩假设为（有最大个不相关的行或列）,则 则代表了矩阵前列所构成的矩阵， 则代表了剩余部分，代表根据需要在前列中选择的一部分列构成的矩阵。

都是对应的奇异值的奇异向量，且 都是按照重要性排列其列向量的。

使用matlab实现对一个矩阵的SVD分解很简单：

1
2
3
4
5
6
7

%%假设X是mxn的矩阵
[U,S,V] = svd(X)
%或者使用
[U,S,V] = svd(X,'econ')
%以及
[U,S,V] = svd(X,0)
%参数econ和0的区别就是在m>n时，svd(X,0)和svd(x,'econ')都只计算前n列U，得出来的S是nxn的矩阵，但在m<n的时候，svd（x,'econ'）只计算V矩阵的前m列，得出来的S是mxm的矩阵。

值得注意的是，任何矩阵都可以进行奇异值分解，未必是方阵

一维向量的回归

伪逆矩阵

对于

假设的秩是r，则

其中称之为 的伪逆矩阵化。

通过这样，我们可以不必直接去计算矩阵 因为矩阵 可能并没有逆。使用$x V_{r}^{r}^{-1}U_{r}b x|Ax-b|{2}$ 的最小化，即求出来的解是最小方差解(least square solution), 并且最小化其均值误差MSE（Mean square error）。

使用SVD对进行线性回归拟合

上节的求逆有什么实际用处呢？

假设我们现在有一个一维数据拟合问题。 将向量进行econmy svd分解，使用Truncated 表示：

即：

求出x为：

等式 中 代表了如何使用左伪逆变化（left pseudo-inverse ）进行对数据集的拟合过程，注意此处的实际上是近似结果，因为使用的 都是Truncated 奇异值。

使用一个matlab历程简单说明如何做拟合：

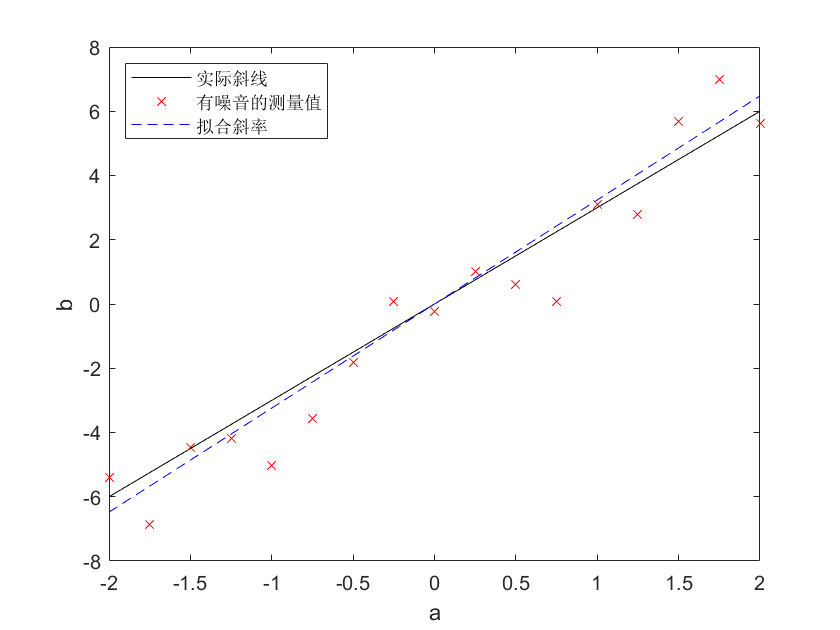
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

%% one dimentional regress
clc
clear all
x = 3; % 真实斜率
a = [-2:.25:2]';
b = a*x + 1*randn(size(a)); % 加入一些噪音
plot(a,x*a,'k') %实际斜线
hold on, plot(a,b,'rx')
%svd 分解
[U,S,V] = svd(a,'econ');%这步得出来的就是近似奇异值分解结果
xtilde = V*inv(S)*U'*b; % 公式（2）得到的拟合值
plot(a,xtilde*a,'b--'); % Plot fit
%画图
xlabel('a')
ylabel('b')
legend({'实际斜线','有噪音的测量值','拟合斜率'},'location','northwest')

图中实线是真实的斜率关系，❌号表示的是对真实斜线有噪音的测量结果，虚线是用 得到的斜率。其本质就是将一个一维向量进行svd分解，然后使用伪逆运算结合有噪音的测量数据进行对真实斜率值进行拟合

上例演示了使用svd方法对一维数据的拟合过程，下一节演示高维数据的拟合过程，其实原理是一样的，都是使用伪逆运算求得采集到的数据集（相当于结果）和对系统的输入量之间的关系，这个关系就是系统的本质属性，在上面的例子中，这个关系就是一维的线性关系，即横坐标和纵坐标之间的映射关系，也就是斜率。之所以可以利用 求得这个线性关系，是因为 本质上就是相当于去模拟一个近似的，然后用这个近似值和相乘（）来得到 ，所以得到的必然是近似解。

高维线性拟合

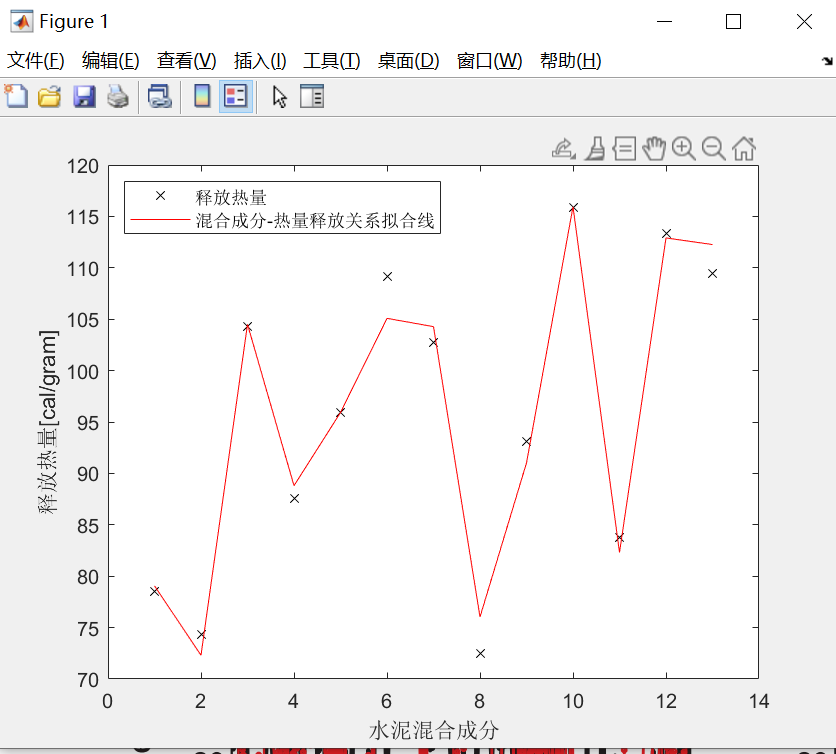
假设有水泥成分和其释放的热量的测量值两个矩阵和 ,现在需要求得其二者之间的关系，假设该关系还是线性的，即符合 式所示的线性关系。

现有 , 使用公式 进行求解拟合关系。

1
2
3
4
5
6
7
8
9

clc,clear all
load hald; % 载入数据
A = ingredients;
b = heat;
[U,S,V] = svd(A,'econ');
x = V*inv(S)*U'*b; % 解 Ax=b 
plot(b,'k'); 
hold on % 画图
plot(A*x,'r-o');