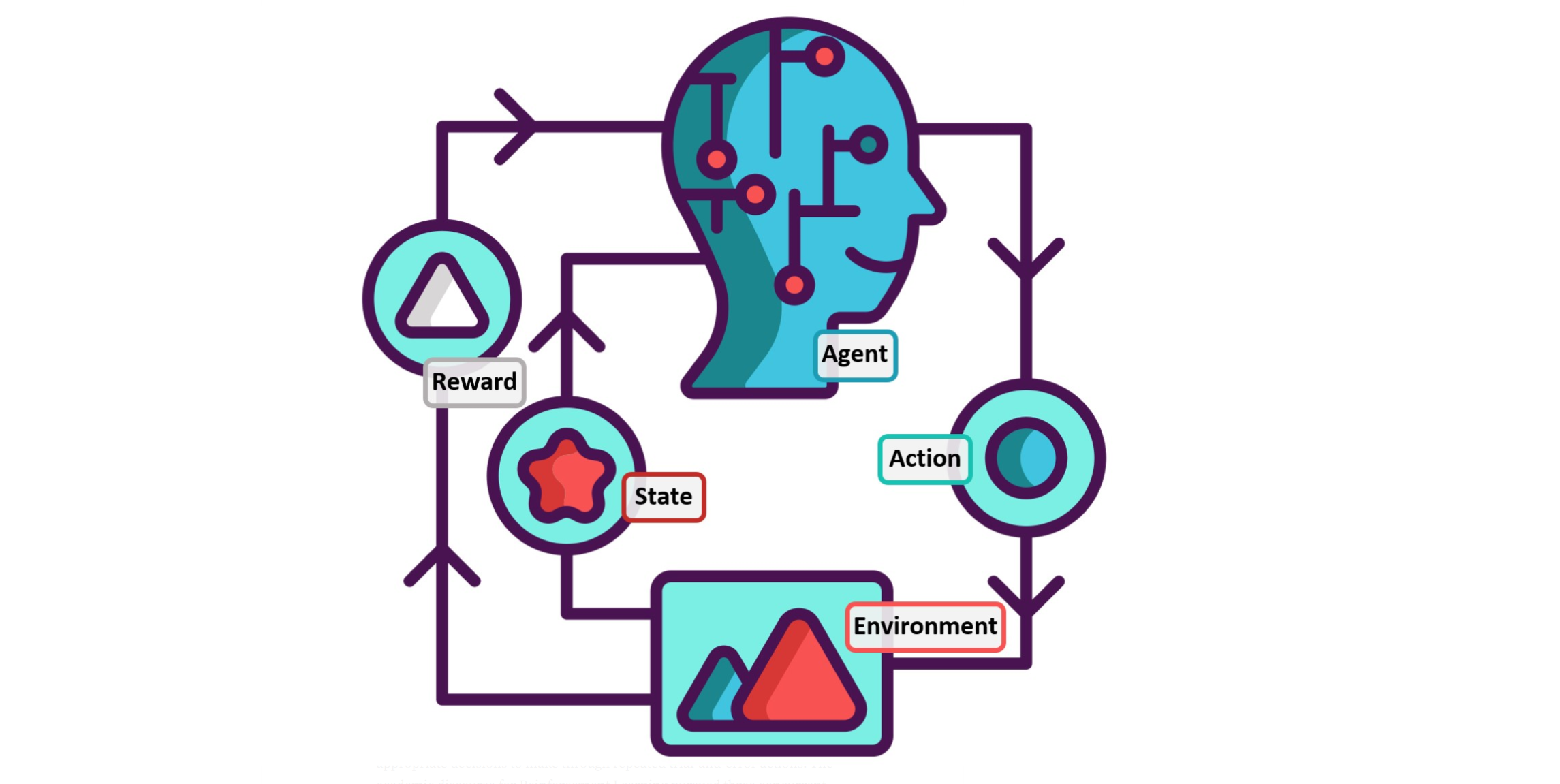
Lecture 4
Epsilon greedy
仔细想了想贪心算法,回顾一下并没有那么简单。贪心算法的定义是:
\[
\begin{equation}
\pi(a \mid s)= \begin{cases}a & \text { with probability }
\frac{\epsilon}{|A|} \\ \arg \max _a Q^\pi(s, a) & \text { with
probability } 1-\epsilon\end{cases}
\end{equation}
\]
也就是使用一个小的概率\(\epsilon\)来决定是探索还是深挖,即以\(\epsilon\)
的概率进行随机动作探索,从而获得那些潜在的可以带来更高未来回报的动作(当前一步不可见,但是在后续步骤中有可能拥有更多回报,也就是潜力更大),以1-\(\epsilon\)
的概率选择最大Q值的动作作为策略更新。
贪心算法是具有递增特性的,即如果对一个本身就是贪心算法进行贪心行为,那么可以得到其递增性,这里不容易想象到具体的案例,但是可以用公式表达:
\[
\begin{ali ...
Lecture 3
Bias, Variance and MSE
偏差、方差、均方差
Consider a statistical model that is parameterized by \(\theta\) and that determines a probability
distribution over observed data \(P(x \mid
\theta)\)
Consider a statistic \(\hat{\theta}\) that provides an estimate of
\(\theta\) and is a function of
observed data \(x \quad
\hat{\theta}=f(x)\)
E.g. for a Gaussian distribution with known variance, the average of
a set of i.i.d data points is an estimate of the mean of the
Gaussian
Definition: the bias o ...
Lecture 2
MRP 马尔科夫奖励过程
\[
\begin{equation}
\left(\begin{array}{c}
V\left(s_1\right) \\
\vdots \\
V\left(s_N\right)
\end{array}\right)=\left(\begin{array}{c}
R\left(s_1\right) \\
\vdots \\
R\left(s_N\right)
\end{array}\right)+\gamma\left(\begin{array}{ccc}
P\left(s_1 \mid s_1\right) & \cdots & P\left(s_N \mid s_1\right)
\\
P\left(s_1 \mid s_2\right) & \cdots & P\left(s_N \mid s_2\right)
\\
\vdots & \ddots & \vdots \\
P\left(s_1 \mid s_N\right) & \cdots & P\left(s_N ...
Multiarmed Bandits问题
多臂老虎机问题
多臂老虎机是假设在玩一个拥有多个摇臂的老虎机,每个摇臂对应一个动作,玩家一次只能选取一个摇臂,相当于是选取了一个动作,描述如下:
老虎机有K个摇臂,每个摇臂以一定的概率吐出金币,且概率是未知的,但服从一定的概率分布即
\[
\mathcal{R}^{a} (r) = \mathbb{P}[r|a]
\]
玩家每次(每个时间步step)只能从K个摇臂中选择其中一个摇臂 \(a \in
\mathcal{A}\),且相邻两次选择或奖励没有任何关系
环境会给出奖励
\[
r_t \sim \mathcal{R}^{a_t}
\]
玩家的目的是通过一定的策略使自己获得的累计奖励最大,即得到更多的金币
\[
\sum_{\tau=1}^t r_\tau
\]
贪心算法选取最优动作Greedy
Algorithm
使用蒙特卡洛算法估计的动作值
\[
\hat{Q}_t(a)=\frac{1}{N_t(a)} \sum_{t=1}^T r_t
\mathbb{1}\left(a_t=a\right)\\
\Rightarro ...
Log-Barrier-method
在求一些优化问题的时候,往往遇到形式如下的问题:
\[
\begin{array}{lll}
\text { Problem statement } & h: \mathbb{R}^{n_x} \rightarrow
\mathbb{R}^{n_h} \\
\min _{x \in \mathbb{R}^{n_x}} & f(\boldsymbol{x}) &
\boldsymbol{g}: \mathbb{R}^{n_x} \rightarrow \mathbb{R}^{n_g} \\
\text { subject to: } & \boldsymbol{h}(\boldsymbol{x})=\mathbf{0}
& \\
& \boldsymbol{g}(\boldsymbol{x}) \leq \mathbf{0}
\end{array}
\]
即需要满足\(x\)在\(h(x)\) 上且 \(g(x) \leq 0\) 时最小化\(f(x)\) 的值。
采用barrier的方法可以求得此解 ...
Active learning 主动学习
Active ADP
active ADP的更新公式
\[
\begin{equation}
U(s)=\max _{a \in A(s)} \sum_{s^{\prime}} P\left(s^{\prime} \mid s,
a\right)\left[R\left(s, a, s^{\prime}\right)+\gamma
U\left(s^{\prime}\right)\right]
\end{equation}
\]
active adp 和passive
adp的主要区别是在于agent在学习效用函数时,对于passive
ADP在某个状态的策略是固定的,对于active
adp在某个状态下有多个动作可以选择,active adp
会选择产生的最大的效用值作为expected utility value(MEU).
exploration and exploitation
智能体对环境的探索依然受到exploration和exploitation的限制,对于使用ADP算法,可以将乐观估计融入效用之更新公式中:
\[
\begin{ ...
Decision Trees决策树
使用Entropy计算率先分割哪个decision
tree的分支
计算一个随机变量的不确定性使用熵,如果一个硬币投掷后头面朝上的概率为1的话,那这个硬币代表的随机变量的不确定性就为0,如果一个硬币有50%的概率投掷硬币头朝上,则其熵计算为:
熵的计算公式:单位为比特
信息增益 information gain
一颗决策树中的非叶子节点有split函数,用于将当前所输入的数据分到左子树或者右子树。我们希望每一个节点的split函数的性能最大化。这里的性能是指把两种不同的数据分开的能力,不涉及到算法的时间复杂度。但是,怎么去衡量一个split函数的性能呢?这里我们使用信息增益来衡量G。如果G越大,说明该节点的split函数将输入数据分成两份的性能越好。
版权声明:本文为CSDN博主「ChainingBlocks」的原创文章 原文链接:https://blog.csdn.net/liangyihuai/article/details/103206360
如果一个decision
tree拥有不同的attribute将一个训练集分割成不同的组 ...
前向网络和反向传播(feedforward
and back-propagation)
激活函数 activation function
网络中每一层除了\(weight \times
x\)的形式,还需要将乘积结果投入一个激活函数中,普适性近似定理universal
approximation
theorem指出,一个只有两层计算单元的网络,第一层是非线性的,第二层是线性的,可以近似任意程度的连续函数。因此激活函数需要是一个非线性的函数。
前向网络中比较流行的的激活函数:
sigmoid:
\[
\sigma(x)=1 /\left(1+e^{-x}\right)
\]
ReLU: rectified linear unit
\[
\operatorname{ReLU}(x)=\max (0, x)
\]
softplus:丝滑版本的ReLU
\[
\operatorname{softplus}(x)=\log \left(1+e^{x}\right)
\]
Tanh
\[
\tanh (x)=\frac{e^{2 x}-1}{e^{2 x}+1}
\]
Note that the ...
Passive
reinforcement learning 被动增强学习
前提:
环境有限,完全可观测,就是说所有的规则都掌握,在环境里所有动作所带来的作用都能够被识别。
对于agent而言,有一个固定的动作执行策略\(\pi(s)\),即在某种环境状态下执行某种动作
agent 的目标是学习贴现效用函数\(U^\pi(s)\)(discounted utility
function) ,这里的\(s\)指的是状态,\(\pi\)是agent的执行策略
贴现效用函数\(U^\pi(s)\)(discounted utility
function) :从初始状态s开始执行策略\(\pi\) 的奖励之和的期望值
4x3 世界模型
使用一个4X3世界的Typical trials 做解释
image-20220425165114825
最上面3行是3个trails,即从(1,1)走到terminal
states的三组走法,概率转换模型为图b所示,这是一个MDP问题,即有概率转换模型、reward、以及状态效用值。
简而言之,被动增强学习是指在某个可被观测的环境中,age ...