首先我们需要知道用于训练减小误差的均值方差公式: \[
\overline{\mathrm{VE}}(\mathbf{w}) \doteq \sum_{s \in \mathcal{S}}
\mu(s)\left[v_\pi(s)-\hat{v}(s, \mathbf{w})\right]^2
\]
其实在目前的研究中,均值方差未必是最好的目标函数,但是现在还没有找到其他更好的函数,且该目标函数是有效的,因此就一直连用了。
Episodic离散情况下的状态分布: \[
\mu(s)=\frac{\eta(s)}{\sum_{s^{\prime}} \eta\left(s^{\prime}\right)},
\quad \text { for all } s \in \mathcal{S}
\] 其中\(\eta\)
表示在每一个状态上的平均停留时间(步): \[
\eta(s)=h(s)+\sum_{\bar{s}} \eta(\bar{s}) \sum_a \pi(a \mid \bar{s}) p(s
\mid \bar{s}, a), \quad \text { for all ...
Policy gradient的表示
A value function may still be used to learn the policy parameter, but
is not required for action selection. We use the notation \(\theta \in \mathbb{R}^{d^{\prime}}\) for
the policy's parameter vector. Thus we write \(\pi(a \mid s,
\boldsymbol{\theta})=\operatorname{Pr}\left\{A_t=a \mid S_t=s,
\boldsymbol{\theta}_t=\boldsymbol{\theta}\right\}\) for the
probability that action \(a\) is taken
at time \(t\) given that the
environment is in state \(s\) at time
\(t\) with paramet ...
MADRL
Deep Reinforcement Learning for Multiagent Systems: A
Review of Challenges, Solutions, and Applications
多Agent系统的深度强化学习:挑战、解决方案和应用综述
Key
Value
文献类型
journalArticle
标题
Deep Reinforcement Learning for Multiagent
Systems: A Review of Challenges, Solutions, and Applications
中文标题
多Agent系统的深度强化学习:挑战、解决方案和应用综述
作者
[[Thanh Thi Nguyen]]、 [[Ngoc Duy
Nguyen]]、 [[Saeid Nahavandi]]
期刊名称
[[IEEE Transactions on Cybernetics]]
DOI
10.1109/TCYB.2020.2977374
引用次数
281 📊
影响因子
19.11 ...
Power method 估计复杂度
power method 的原理,其实就是利用矩阵的性质得到最大特征值的表达式
实例
Many-Agent Reinforcement Learning-chapter
4
多智能体强化学习-1
Key
Value
文献类型
journalArticle
标题
Many-Agent Reinforcement Learning
中文标题
多代理强化学习
作者
[Yaodong Yang]
评分
⭐⭐⭐⭐⭐
分类
[[A 多智能体增强学习, 0 综述]]
条目链接
My Library
PDF 附件
2021__Yang__Many-Agent Reinforcement
Learning.pdf
👣➿👣
Alpha rank :
Mathmatical formulation
假设有\(N\)个agent,每个agent有\(k_i\)个策略,则有
单个智能体的策略集 \(\mathscr{S}_i\) , 大小为\(k_i\): \(\mathscr{S}_i=\left\{\pi_{i, 1}, \ldots, \pi_{i,
k_i}\right\}, k_i=\left|\mathscr{ ...
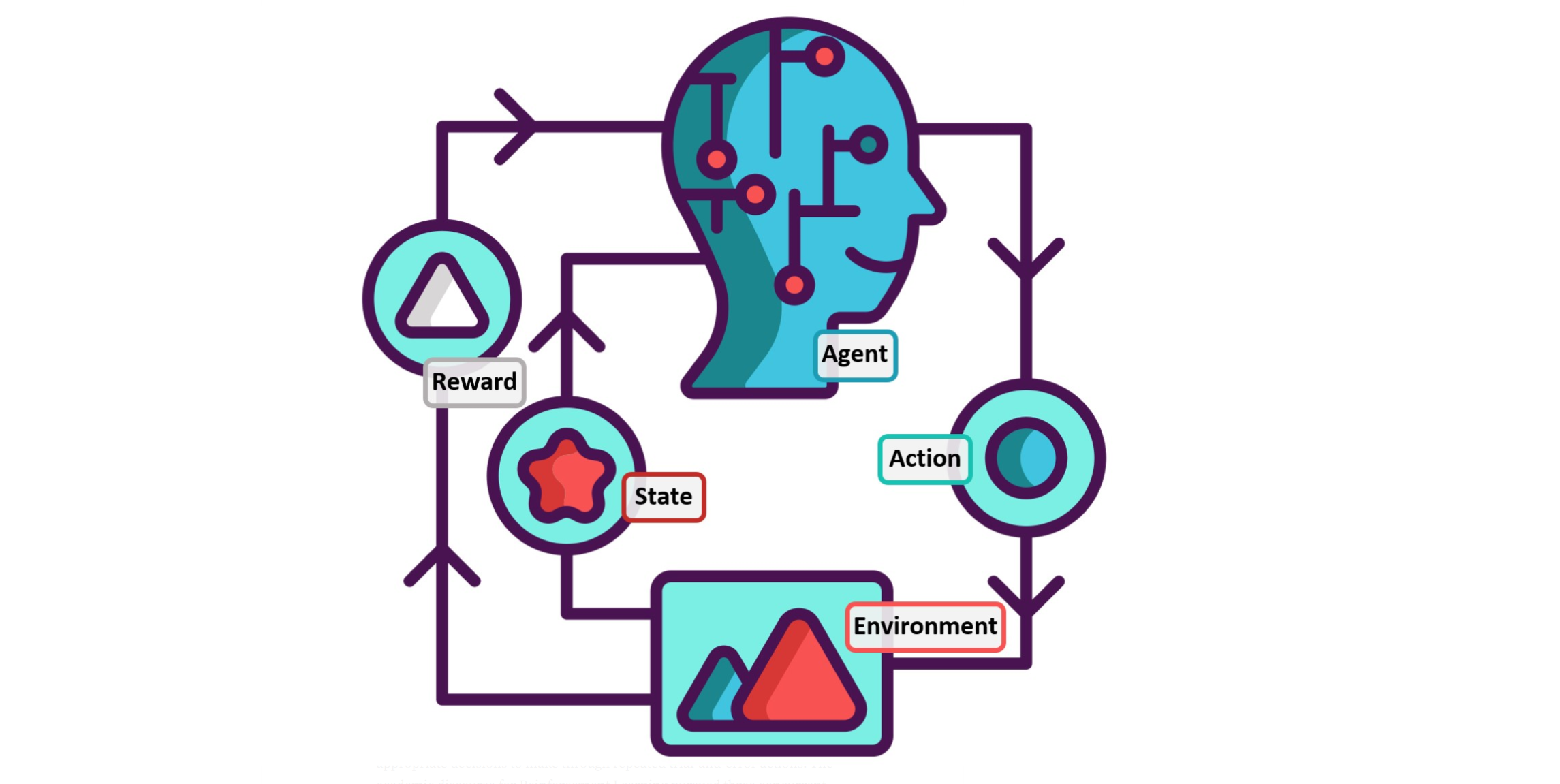
Single-Agent RL
Markov process 马尔科夫过程
image-20220505143413803
马尔科夫过程是一个标准模型,广泛应用在全观测状态系统中,即智能体可以完全获取环境的状态信息,通过概率转换模型,在某一个状态通过一个动作到达另一个状态。因此结局马尔科夫问题的关键就是找到一个策略使得动作空间\(A\)映射到状态空间\(S\)上去。其中动作为\(a_{t} \sim \pi\left(\cdot \mid
s_{t}\right)\) ,并能使得到达每一个状态获取的回报discounted
accumulated reward能够被最大化:
\[
\mathbb{E}\left[\sum_{t \geq 0} \gamma^{t} R\left(s_{t}, a_{t},
s_{t+1}\right) \mid a_{t} \sim \pi\left(\cdot \mid s_{t}\right),
s_{0}\right]
\]
其中action-value function(Q方程)和state-value function
(V方程)分别为 ...
第二章
拉普拉斯矩阵
Jordan form matrix and transformation matrix
特征值
和右特征向量 满足
Theorem 2.1 L has rank N-1, i.e., is nonrepeated, if and only if
graph G has a spanning tree
如果一个图G的拉普拉斯矩阵的秩是N-1,则 不重复的条件是 图G含有spanning tree,spanning
tree是指该图有不只一个子树包含图中所有的顶点
且有以下推论:
因为
所有的行自相加等于0,所以有
$$
$$
L c=0
$$
$$
其中,
是任意一个常数,这代表了每个矩阵必然含有特征值对应有特征向量,所以,即拉普拉斯矩阵的零空间里必含。
如果的维度是1,即拉普拉斯矩阵的秩为
,则是该拉普来说矩阵无重复的特征值,且所对应的是其零空间内唯一的特征向量。
⭐️拉普拉斯矩阵必然含有
⭐️如果图是强连接图,则图必有spanning
tree且其拉普拉斯矩阵的秩为
⭐️如果图有spanning tree,则
⭐️如果图有spanning ...